For two inputs \(X_{1}\) and \(X_{2}\) and output \(Y\), a constant elasticity of substitution (CES) production function is given by

where \(\alpha>0\) is an efficiency parameter, \(\eta>0\) is a returns to scale parameter, \(ho>-1\) is a substitution parameter, and \(0

a. Using nonlinear least squares, estimate the following log form of the CES function

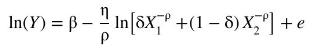
where \(\beta=\ln (\alpha)\). Report your results and standard errors. [Hint: If you run into difficulties, try using 0.5 as the starting value for all of your parameters.]

b. Find \(95 \%\) interval estimates for \(\alpha, \eta, \varepsilon\), and \(\delta\).

c. Using a \(5 \%\) significance level, test the null hypothesis \(H_{0}: \eta=1, ho=0\) against the alternative \(H_{1}: \eta eq 1\) or \(ho eq 0\). Does a constant-returns-to-scale Cobb-Douglas function appear to be adequate?

Transcribed Image Text:

Y = [8 + (1 ) -n/p -