In Example 7.11, we used the linear probability model to check whether students were assigned randomly to small classes in Project STAR. In this exercise, we use multinomial logit and the data file star to explore the issue.

a. Create the variable \(C L A S S=1\) for a regular sized class, \(C L A S S=2\) for a small class, and \(C L A S S=3\) for a regular sized class with a teacher aide. What percentage of the students in the sample were assigned to each type of class?

b. Estimate a multinomial logit model explaining CLASS with explanatory variables \(B O Y\), WHITE_ASIAN, BLACK, FREELUNCH, SCHURBAN, and SCHRURAL. Use CLASS \(=1\), the regular class, as the base group. If students are assigned randomly what values should the model coefficients take? Are any of the estimated coefficients significantly different from zero at the \(5 \%\) level?

c. Find the ratio of the probability of being in a small class for a white boy who receives lunch if his school is in a rural area, relative to the probability of him being in a regular sized class.

d. Find the ratio of the probability of being in a regular sized class with a teacher aide for a white boy who receives lunch if his school is in a rural area, relative to the probability of him being in a regular sized class.

e. Carry out a likelihood ratio test that the coefficients of BOY, WHITE_ASIAN, BLACK, FREELUNCH, and SCHURBAN are zero, against the alternative that they are not, at the 5\% level. What is the \(5 \%\) critical value for this test?

f. Carry out a likelihood ratio test that the coefficients of BOY, WHITE_ASIAN, BLACK, FREELUNCH, SCHURBAN, and SCHRURAL are zero, against the alternative that they are not, at the \(5 \%\) level. What is the \(5 \%\) critical value for this test?

g. Based on the outcomes of parts (a)-(f), what do you conclude about random assignment of students in Project STAR?

Data From Example 7.11:-

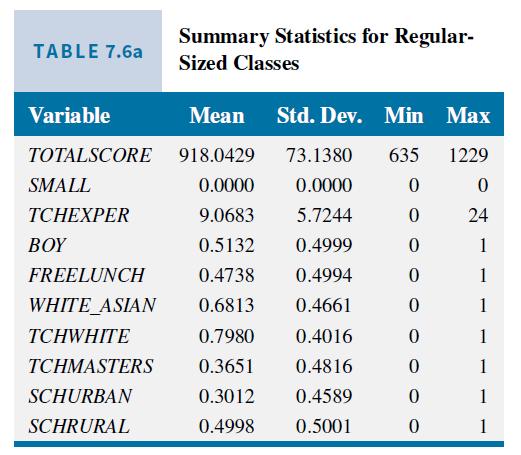
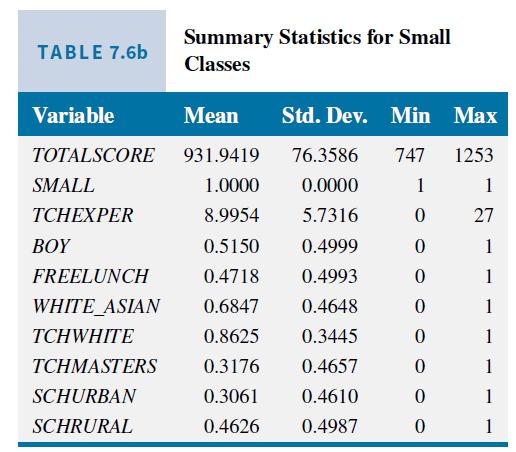
In Table 7.6a and b, we examined the summary statistics for the data sorted by whether pupils were in a regular class or a small class. Except for TOTALSCORE, we did not find much difference in the sample means of the variables examined. Another way to check for random assignment is to regress SMALL on these characteristics and check for any significant coefficients, or an overall significant relationship. If there is random assignment, we should not find any significant relationships. Because SMALL is an indicator variable, we use the linear probability model discussed in Section 7.4. The estimated linear probability model is 

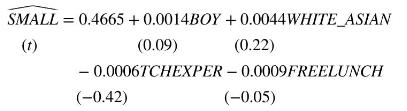
First, note that none of the right-hand-side variables are statistically significant. Second, the overall \(F\)-statistic for this linear probability model is 0.06 with a \(p=0.99\). There is no evidence that students were assigned to small classes based on any of these criteria. Also, recall that the linear probability model is so named because \(E(S M A L L \mid \mathbf{X})\) is the probability of observing \(S M A L L=1\) in a random draw from the population. If the coefficients of all the potential explanatory factors are zero, the estimated intercept gives the estimated probability of observing a child in a small class to be 0.4665 , with \(95 \%\) interval estimate \([0.4171,0.5158]\). We cannot reject the null hypothesis that the intercept equals 0.5 , which is what it should be if students are allocated by a "flip" of a coin. The importance of this, again, is that by randomly assigning students to small classes we can estimate the "treatment" effect using the simple difference estimator in (7.15). The ability to isolate the important class size effect is a powerful argument in favor of randomized controlled experiments.

Data From Equation 7.15:-

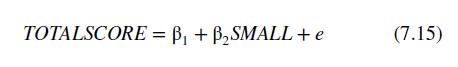
Data From Table 7.6a:-

Transcribed Image Text:

SMALL = 0.4665+ 0.0014BOY +0.0044WHITE ASIAN (0.09) (0.22) -0.0006TCHEXPER - 0.0009 FREELUNCH (t) (-0.42) (-0.05)