In Chapter 7, we examined the Tennessee's Project STAR. In the experiment, children were randomly assigned within
Question:
In Chapter 7, we examined the Tennessee's Project STAR. In the experiment, children were randomly assigned within schools into three types of classes: small classes with 13-17 students, regular sized classes with 22-25 students, and regular sized classes with a full-time teacher aide to assist the teacher. In Example 7.11, we checked for random assignment of children to the three types of classes using a linear probability model, regressing the indicator SMALL (small class) on student characteristics. Let us reconsider this regression using logit rather than the linear probability model. If there is random assignment of children to types of classes, then we should not find any significant relationships. Use data file star5_small2 for this exercise. The data file star5 contains more observations.
a. Estimate a logit model with outcome variable \(S M A L L\) and explanatory variables \(B O Y\) and \(B L A C K\). Individually test the coefficients of these variables for significance. What do you find? Test the coefficients jointly for significance using the likelihood ratio test. What do you find? Can we reject the null hypothesis that assignment to small classes is done randomly?
b. Repeat the estimation and testing in part (a) using outcome variables AIDE and REGULAR. Do you find any evidence that students were not randomly assigned?
c. Add the variable FREELUNCH to the models in (a) and (b) and reestimate them. Do you find any evidence that there is a systematic pattern between class assignment and this variable?
d. Add the two variables TCHWHITE and TCHMASTERS to the models in (c) and reestimate them. In each, carry out a likelihood ratio test for the joint significance of TCHWHITE and TCHMASTERS. What do you conclude? In the experiment students were randomized within schools but not across schools. Does this offer any explanation of your findings? If so, how?
Data From Example 7.11:-
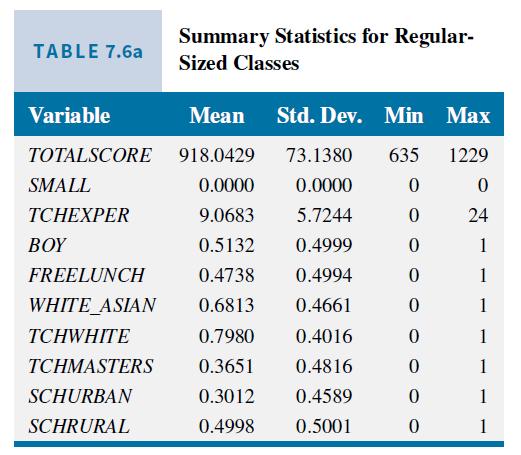
In Table 7.6a and b, we examined the summary statistics for the data sorted by whether pupils were in a regular class or a small class. Except for TOTALSCORE, we did not find much difference in the sample means of the variables examined. Another way to check for random assignment is to regress SMALL on these characteristics and check for any significant coefficients, or an overall significant relationship. If there is random assignment, we should not find any significant relationships. Because SMALL is an indicator variable, we use the linear probability model discussed in Section 7.4. The estimated linear probability model is
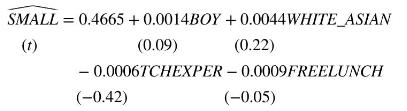
First, note that none of the right-hand-side variables are statistically significant. Second, the overall \(F\)-statistic for this linear probability model is 0.06 with a \(p=0.99\). There is no evidence that students were assigned to small classes based on any of these criteria. Also, recall that the linear probability model is so named because \(E(S M A L L \mid \mathbf{X})\) is the probability of observing \(S M A L L=1\) in a random draw from the population. If the coefficients of all the potential explanatory factors are zero, the estimated intercept gives the estimated probability of observing a child in a small class to be 0.4665 , with \(95 \%\) interval estimate \([0.4171,0.5158]\). We cannot reject the null hypothesis that the intercept equals 0.5 , which is what it should be if students are allocated by a "flip" of a coin. The importance of this, again, is that by randomly assigning students to small classes we can estimate the "treatment" effect using the simple difference estimator in (7.15). The ability to isolate the important class size effect is a powerful argument in favor of randomized controlled experiments.
Data From Equation 7.15:-
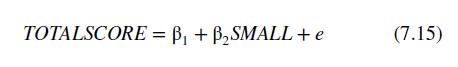
Data From Table 7.6a:-
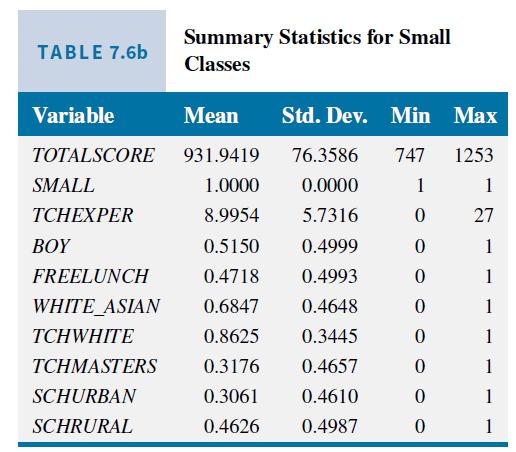
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim




