Consider a regression explaining the share of Olympic Games medals won by each country in 1988 (in
Question:
Consider a regression explaining the share of Olympic Games medals won by each country in 1988 (in Seoul, South Korea), 1992 (in Barcelona, Spain), and 1996 (in Atlanta, GA, USA) as a function of \(L P O P=\ln (P O P)=\) the logarithm of population in millions, \(L G D P=\ln (G D P)=\) the logarithm of gross domestic product (in billions of 1995 dollars), and HOST, an indicator variable \(=1\) for the country hosting the Olympics. The total number of medals awarded in 1988 was 738; in 1992, there were 815 medals awarded, and in 1996, 842 medals were awarded. Using the total number of medals awarded, we compute the percentage share of medals (SHARE) won by each country.
a. The least squares estimates of \(S H A R E=\beta_{1}+\beta_{2} \ln (P O P)+\beta_{3} \ln (G D P)+\beta_{4} H O S T+e\) are in Table 16.15. Are the signs and significance of the coefficient estimates reasonable?
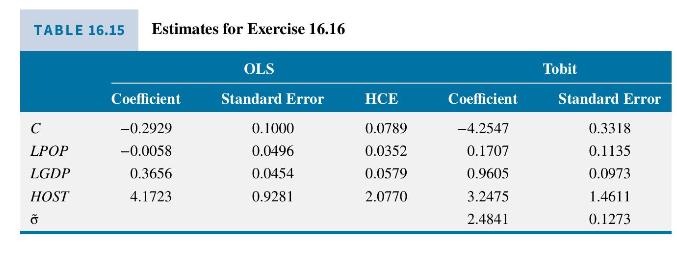
b. Using the OLS estimates, what is the predicted effect of \(G D P\) on the expected share of medals won? That is, how much do we predict the share of medals won will change if GDP increases by \(1 \%\) ? Construct a \(95 \%\) interval estimate of this effect.
c. For the model estimated by OLS, the robust Breusch-Pagan LM test statistic for heteroskedasticity as a function of \(\ln (G D P)\) is \(N R^{2}=32.80\). What can we conclude about the OLS estimator and the usual standard errors based on this test?
d. We also report the OLS heteroskedasticity robust standard errors (HCE) in Table 16.15. Construct a \(95 \%\) interval estimate for the predicted effect of a \(1 \%\) increase in GDP on the share of medals won using the robust standard errors.
e. Among the 508 countries competing in these summer Olympics, almost \(62 \%\) won no medals. Does this cause any potential problems for the least squares estimator? By using robust standard errors in part (c), we have solved any problems with the OLS estimator. True or false? Explain your choice.
f. Compare the Tobit parameter estimates reported in Table 16.15 to the OLS estimates and standard errors. What are the differences? Is Tobit a reasonable estimator for the share of medals won in this example? Why?
g. Using the Tobit estimates, what is the estimated effect of \(G D P\) on the expected share of medals won for a nonhost country with \(G D P=150\) billion and \(P O P=30\) million? That is, how much do we estimate the expected share of medals won will change if GDP increases by one percent? In equation (16.35), let \(y=\) SHARE and \(x=\ln (G D P)\). Then
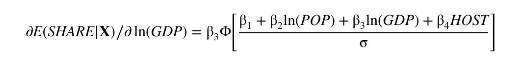
Also, \(\partial \ln (G D P) / \partial G D P=1 / G D P\). Then refer to the analysis of the linear-log model in Section 4.3.3.
Data From Equation 16.35:-
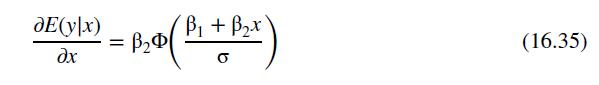
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





