Consider a Poisson regression explaining the number of Olympic Games medals won using data from 1988 (in Seoul, South Korea) and 1992 (in Barcelona, Spain) by various countries as a function of \(L P O P=\ln (P O P)=\) the logarithm of population in millions, and \(L G D P=\ln (G D P)=\) the logarithm of gross domestic product (in billions of 1995 dollars). That is, \(E(M E D A L T O T \mid \mathbf{X})=\exp \left[\beta_{1}+\beta_{2} \ln (P O P)+\beta_{3} \ln (G D P)\right]\). The estimated coefficients, using 316 observations, are in Table 16.14, Model 1.

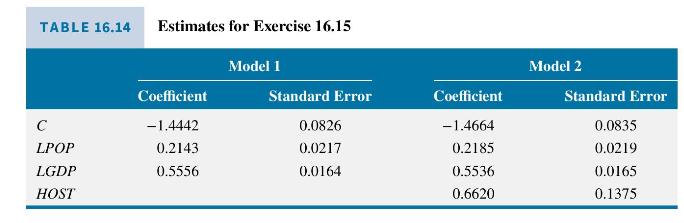
a. Using Model 1 results, what is the estimated impact on the number of medals won if \(G D P\) increases by \(1 \%\) ? [Hint: It can be shown (can you?) that \(\beta_{3}\) is an elasticity.]

b. In 1996, Bulgaria had \(G D P=11.8\) billion and a population of 8.356 million. Estimate the expected number of medals that Bulgaria would win in the Olympics, held in Atlanta, USA. They did win 15 medals.

c. Calculate the probability that Bulgaria in 1996 would win one or fewer medals.

d. In 1996, Switzerland had \(G D P=306\) billion and a population of 6.875 million. Estimate the expected number of medals that Switzerland would win. They did win 1 medal.

e. Calculate the probability that Switzerland in 1996 would win one or fewer medals.

f. HOST is an indicator variable \(=1\) for the country hosting the Olympics. This variable is added in Model 2. Interpret its coefficient. [Hint: What is the estimated percentage change in the conditional mean?] Is the estimated effect large or small? Is the coefficient statistically significant at the \(1 \%\) level?

g. In 1996, the Olympic games were held in the U.S. city of Atlanta, GA. In that year, the U.S. population was 265 million and its GDP was 7280 billion. Estimate the expected number of medals the United States would win using Model 1 and again using Model 2. The United States won 101 medals that year. Which model's estimated value was closer to the true outcome?

Transcribed Image Text:

TABLE 16.14 Estimates for Exercise 16.15 Model 1 Model 2 Coefficient Standard Error Coefficient Standard Error C -1.4442 0.0826 -1.4664 0.0835 LPOP 0.2143 0.0217 0.2185 0.0219 LGDP 0.5556 0.0164 0.5536 0.0165 HOST 0.6620 0.1375