In the new Keynesian Phillips curve (NKPC), inflation at time (tleft(I N F_{t} ight)) depends on inflationary

In the new Keynesian Phillips curve (NKPC), inflation at time \(t\left(I N F_{t}\right)\) depends on inflationary expectations formed at time \(t\) for time \(t+1\left(\right.\) INFEX \(\left.X_{t}\right)\), and the output gap, defined as output less potential output. Expectations of higher inflation lead to greater inflation. The closer output is to potential output, the higher the inflation rate. Amberger et al. \({ }^{21}\) compare results from estimating NKPCs with two output gaps, one that has been augmented with changes in financial variables \(\left(F N G A P_{t}\right)\), and one that has not \(\left(G A P_{t}\right)\). Quarterly data for Italy for the period 1990Q1 to 2014Q4 can be found in the data file italy.

a. Using OLS, estimate the two equations

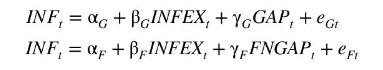
Find 95\% interval estimates for \(\gamma_{G}\) and \(\gamma_{F}\) using both conventional and HAC standard errors. Comment on (i) the relative widths of the intervals with and without HAC standard errors and (ii) whether one output gap measure is preferred over another in terms of its impact on inflation.

b. What are the values of the first four residual autocorrelations from each of the two regressions in part (a)? Which ones are significantly different from zero at a \(5 \%\) significance level?

c. Consider the generic equation \(y_{t}=\alpha+\beta x_{t}+\gamma z_{t}+e_{t}\) with \(\operatorname{AR}(2)\) errors \(e_{t}=\psi_{1} e_{t-1}+\psi_{2} e_{t-2}+v_{t}\) where the \(v_{t}\) are not autocorrelated. Show that this model can be written as

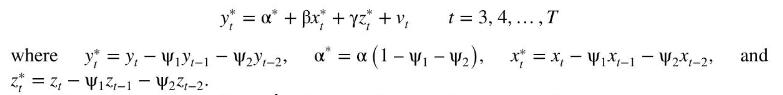
d. Using the least squares residuals \(\hat{e}_{G t}\) from the first equation in part (a), estimate \(\psi_{1}\) and \(\psi_{2}\) from the regression equation \(\hat{e}_{G t}=\psi_{1} \hat{e}_{G, t-1}+\psi_{2} \hat{e}_{G, t-2}+\hat{v}_{t}\). Along the lines of the transformations in part (c), use the estimates of \(\psi_{1}\) and \(\psi_{2}\) to find transformed variables \(I N F_{t}^{*}, I N F E X_{t}^{*}\), and \(G A P_{t}^{*}\) and then estimate \(\alpha_{G}^{*}, \beta_{G}\), and \(\gamma_{G}\) from the transformed equation \(I N F_{t}^{*}=\alpha_{G}^{*}+\beta_{G} I N F E X_{t}^{*}+\) \(\gamma_{G} G A P_{t}^{*}+v_{t}\). Estimate the equation with both conventional and HAC standard errors.

e. Using the results from part (d), find \(95 \%\) interval estimates for \(\gamma_{G}\) using both conventional and HAC standard errors. Comment on (i) the relative widths of the intervals with and without HAC standard errors and (ii) how the estimates and intervals compare with the corresponding ones obtained in part (a).

Transcribed Image Text:

INF = ac+BINFEX, + YG GAP, + eGt = INF, F+BFINFEX, +1FNGAP, + eft