In this exercise, we generalize the results in Exercise 16.5. Consider a logit model with only an
Question:
In this exercise, we generalize the results in Exercise 16.5. Consider a logit model with only an intercept, \(P(y=1)=\Lambda\left(\gamma_{1}\right)\), where \(\Lambda(\bullet)\) is the logistic \(c d f\). Suppose in a sample of \(N\) observations, there are \(N_{1}\) values \(y_{i}=1\) and \(N_{0}\) values \(y_{i}=0\).
a. Show that the logit log-likelihood function is \(\ln L\left(\gamma_{1}\right)=N_{1} \ln \Lambda\left(\gamma_{1}\right)+N_{0} \ln \left[1-\Lambda\left(\gamma_{1}\right)\right]\).
b. Show that \(d \ln L\left(\gamma_{1}\right) / d \gamma_{1}=N_{1} \lambda\left(\gamma_{1}\right) / \Lambda\left(\gamma_{1}\right)-N_{0} \lambda\left(\gamma_{1}\right) /\left[1-\Lambda\left(\gamma_{1}\right)\right]\), where \(\lambda(\cdot)\) is given in (16.6).
c. Setting the derivative in (b) to zero and solving, show that \(\Lambda\left(\tilde{\gamma}_{1}\right)=N_{1} / N\). What is the interpretation of \(N_{1} / N\) ? [Note: This does not require you to first solve for \(\tilde{\gamma}_{1}\), the MLE.]
d. Using (c) show that \(\ln L\left(\tilde{\gamma}_{1}\right)=N_{1} \ln \left(N_{1} / N\right)+N_{0} \ln \left(N_{0} / N\right)\).
e. Show that a probit model, \(P(y=1)=\Phi\left(\gamma_{1}\right)\), where \(\Phi(\bullet)\) is the standard normal \(c d f\), results in the same value for the log-likelihood as in part (d).
Data From Equation 16.6:-
![]()
Data From Exercise 16.5:-
We are given three observations on binary choice with \(y_{1}=1, y_{2}=1, y_{3}=0\). Consider a logit model with only an intercept, \(P(y=1)=\Lambda\left(\gamma_{1}\right)\), where \(\Lambda(\bullet)\) is the logistic \(c d f\).
a. Show that the log-likelihood function is \(\ln L\left(\gamma_{1}\right)=2 \ln \Lambda\left(\gamma_{1}\right)+\ln \left[1-\Lambda\left(\gamma_{1}\right)\right]\).
b. Show that \(d \ln L\left(\gamma_{1}\right) / d \gamma_{1}=2 \lambda\left(\gamma_{1}\right) / \Lambda\left(\gamma_{1}\right)-\lambda\left(\gamma_{1}\right) /\left[1-\Lambda\left(\gamma_{1}\right)\right]\), where \(\lambda(\cdot)\) is the logistic \(p d f\) in (16.14).
c. The value of \(\gamma_{1}\) such that \(d \ln L\left(\gamma_{1}\right) / d \gamma_{1}=0\) is the maximum likelihood estimator \(\tilde{\gamma}_{1}\). True, false, or maybe?
d. It can be shown that for the logit model \(\ln L\left(\gamma_{1}\right)\) is strictly concave, meaning that the second derivative is negative for all values of \(\gamma_{1}\) or \(d^{2} \ln L\left(\gamma_{1}\right) / d \gamma_{1}{ }^{2}
(c) now?
e. Setting the derivative in
(c) to zero and solving, show that \(\Lambda\left(\tilde{\gamma}_{1}\right)=2 / 3\). [Note: This does not require you to first solve for \(\tilde{\gamma}_{1}\).]
f. Now, solve the condition in
(c) to show that \(\tilde{\gamma}_{1}=-\ln (1 / 2)\).
Data From Equation 16.14:-
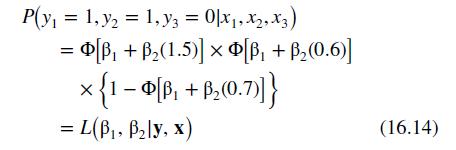
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





