Inflationary expectations play an important role in wage negotiations between employers and employees. In this exercise, we examine how inflationary expectations of Australian businesses, collected by National Australia Bank surveys, depend on past inflation rates. The data are quarterly and run from 1989Q3 to 2016Q1. The basic model being estimated is

where \(E X P N_{t}\) is the expected percentage price increase for 3 months ahead and \(I N F_{t-1}\) is the inflation rate in the previous 3 months. The left-hand panel of estimates in Table 9.12 contains OLS estimates of \(\alpha\) and \(\beta_{1}\) with conventional and HAC standard errors. The right-hand panel contains nonlinear least squares estimates and both sets of standard errors assuming the equation errors follow the AR(1) process \(e_{t}=ho e_{t-1}+v_{t}\). The first three sample autocorrelations of the residuals are also reported for

a. What evidence is there of serial correlation in the errors \(e_{t}\) ? What is the impact of any serial correlation on interval estimation of \(\beta_{1}\) ?

b. Is there any evidence of remaining serial correlation in the errors \(v_{t}\) after estimating the model with an AR(1) error?

c. What is the impact of the \(\operatorname{AR}(1)\) error assumption on the estimate for \(\beta_{1}\) ? Suggest a reason for the large difference in magnitude.

d. Show that the AR(1) error model can be written as

where \(\delta=\alpha(1-ho), \theta_{1}=ho, \delta_{1}=\beta_{1}\) and \(\delta_{2}=-ho \beta_{1}\).

e. Estimating the unconstrained version of the model in part (d) via OLS yields

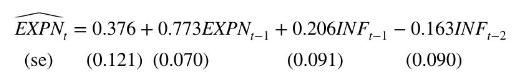
Given that \(\operatorname{se}\left(\hat{\theta}_{1} \hat{\delta}_{1}+\hat{\delta}_{2}\right)=0.1045\), test the hypothesis \(H_{0}: \theta_{1} \delta_{1}=-\delta_{2}\) using a \(5 \%\) significance level. What is the implication of this test result?

f. Find estimates for the first four lag coefficients of the infinite distributed lag representation of the equation estimated in part (e).

Transcribed Image Text:

== EXPN, a+B INF+e, 1-1