Knowledge is Power Program (KIPP) Schools are charter schools with largely minority students. These schools differ in a number of ways from public schools, but emphasize longer days and more time spent in school. The question is: "How much benefit is there to attending a KIPP school?"

a. Let \(y_{i}=M A T H_{i}\) be the outcome of a math achievement test. This outcome is standardized by subtracting the average and dividing by the standard deviation, so that \(y=0\) is the average score, and \(y=1\) is a score that is one standard deviation above average, and so on. Let \(x_{i}=\) ATTENDED \(_{i}\) be an indicator variable with the value one if a student attended a KIPP school and zero otherwise. In the regression \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}\), suppose that the OLS estimate of \(\beta_{2}\) is \(b_{2}=0.467\), with a standard error of 0.103 . Based on this regression result, does attending a KIPP school seem to improve math test score? Is the estimate of the amount of improvement a meaningful amount? If the average math score of those attending the KIPP school is 0.095 , what is the average score of those who do not attend the KIPP school?

b. Explain why we might worry that ATTENDED is an endogenous variable.

c. Offers of admission are randomly assigned to the pool of KIPP applicants. Some of those offered admission wind up attending and some do not. Let WINNER be an indicator variable taking the value one if a student receives an offer to attend, and zero otherwise. Suppose that \(78.7 \%\) of offers to attend are accepted. Does WINNER satisfy the conditions for an instrumental variable?

d. Suppose that \(z_{i}=W I N N E R_{i}\). In the terms of this example, explain the components of

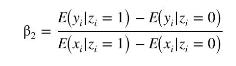
See Exercises 10.4 and 10.5 for background discussion of the expression.

e. The average math score of those receiving an offer to attend the KIPP school was -0.003 , which is very close to average. The average score of those not offered a seat was -0.358 , which is about one-third of a standard deviation below average. Interestingly, some students wind up attending the KIPP school despite not being randomly selected from the applicants. Assume that the proportion of students attending the KIPP school who were not "winners" be \(4.6 \%\). Obtain the Wald estimator of \(\beta_{2}\) by replacing the population averages in part (d) with sample averages. How does this estimate compare to the OLS estimate in part (a)? Does attending a KIPP school appear to have a meaningful positive effect on scores of those attending?

Data From Exercise 10.4:-

Suppose that \(x\) is endogenous in the regression \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}\). Suppose that \(z_{i}\) is an instrumental variable that takes two values, one and zero; it is an indicator variable. Make the assumption \(E\left(e_{i} \mid z_{i}\right)=0\).

a. Show that \(E\left(y_{i} \mid z_{i}\right)=\beta_{1}+\beta_{2} E\left(x_{i} \mid z_{i}\right)\).

b. Assume \(E\left(x_{i} \mid z_{i}\right) eq 0\). Does \(z_{i}\) satisfy conditions IV1-IV3? Explain.

c. Write out the conditional expectation in (a) for the two cases with \(z_{i}=1\) and \(z_{i}=0\). Solve the two resulting equations for \(\beta_{2}\).

d. Suppose we have a random sample \(\left(y_{i}, x_{i}, z_{i}\right), i=1, \ldots, N\). Give an intuitive argument that a consistent estimator of \(E\left(y_{i} \mid z_{i}=1\right)\) is the sample average of the \(y_{i}\) values for the subset of observations for which \(z_{i}=1\), which we might call \(\bar{y}_{1}\).

e. Following the strategy in part (d) form \(\bar{y}_{1}, \bar{y}_{0}, \bar{x}_{1}\), and \(\bar{x}_{0}\). Show that the empirical implementation of the expression in (c) is \(\hat{\beta}_{\text {WALD }}=\left(\bar{y}_{1}-\bar{y}_{0}\right) /\left(\bar{x}_{1}-\bar{x}_{0}\right)\), which is the Wald Estimator, in honor of Abraham Wald.

f. Explain how \(E\left(x_{i} \mid z_{i}=1\right)-E\left(x_{i} \mid z_{i}=0\right)\) might be viewed as a measure of the strength of the instrumental variable \(z_{i}\).

Data From Exercise 10.5:-

Suppose that \(x_{i}\) is endogenous in the regression \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}\). Suppose that \(z_{i}\) is an instrumental variable that takes two values, one and zero with probabilities \(p\) and \(1-p\), respectively, that is, \(\operatorname{Pr}\left(z_{i}=1\right)=p\) and \(\operatorname{Pr}\left(z_{i}=0\right)=1-p\).

a. Show that \(E\left(z_{i}\right)=p\).

b. Show that \(E\left(y_{i} z_{i}\right)=p E\left(y_{i} \mid z_{i}=1\right)\).

c. Use the law of iterated expectations to show that \(E\left(y_{i}\right)=p E\left(y_{i} \mid z_{i}=1\right)+(1-p) E\left(y_{i} \mid z_{i}=0\right)\).

d. Substitute (a), (b), and (c) results into \(E\left(y_{i} z_{i}\right)-E\left(y_{i}\right) E\left(z_{i}\right)\) to show that \(\operatorname{cov}\left(y_{i}, z_{i}\right)=p(1-p) E\left(y_{i} \mid z_{i}=1\right)-p(1-p) E\left(y_{i} \mid z_{i}=0\right)\).

e. Use the arguments in (a)- (d) to show that \(\operatorname{cov}\left(x_{i}, z_{i}\right)=p(1-p)\left[E\left(x_{i} \mid z_{i}=1\right)-E\left(x_{i} \mid z_{i}=0\right)\right]\).

f. Assuming \(E\left(e_{i}\right)=0\) show \(\left[y_{i}-E\left(y_{i}\right)\right]=\beta_{2}\left[x_{i}-E\left(x_{i}\right)\right]+e_{i}\).

g. Multiply both sides of the expression in (f) by \(z_{i}-E\left(z_{i}\right)\) and take expectations to show \(\operatorname{cov}\left(y_{i}, z_{i}\right)=\beta_{2} \operatorname{cov}\left(x_{i}, z_{i}\right)\) if \(\operatorname{cov}\left(e_{i}, z_{i}\right)=0\).

h. Using (d), (f), and (g) show that \(\beta_{2}=\frac{E\left(y_{i} \mid z_{i}=1\right)-E\left(y_{i} \mid z_{i}=0\right)}{E\left(x_{i} \mid z_{i}=1\right)-E\left(x_{i} \mid z_{i}=0\right)}\)

i. Show that the empirical implementation of (h) leads to \(\hat{\beta}_{W A L D}=\left(\bar{y}_{1}-\bar{y}_{0}\right) /\left(\bar{x}_{1}-\bar{x}_{0}\right)\).

Transcribed Image Text:

E(ylz, 1) E(xz, = 1) E(ylz, = 0) E(xz, = 0)