The file collegetown contains data on 500 single-family houses sold in Baton Rouge, Louisiana during 2009-2013. We will be concerned with the selling price in thousands of dollars (PRICE), and the size of the house in hundreds of square feet (SQFT). Use all observations to estimate the following regression model:

Suppose that assumptions MR1-MR6 all hold. In particular, \((e \mid S Q F T) \sim N\left(0, \sigma^{2}\right)\).

a. Report the results. Are the estimated coefficients significantly different from zero?

b. Write down an expression for the marginal effect \(\partial E[\ln (P R I C E \mid S Q F T)] / \partial S Q F T\). Discuss the nature of this marginal effect and the expected signs for \(\beta_{2}\) and \(\beta_{3}\).

c. Find and interpret point and \(95 \%\) interval estimates for \(\partial E[\ln (\) PRICE SQFT \()] / \partial S Q F T\) for houses with (i) 1500 square feet, (ii) 3000 square feet, and (iii) 4500 square feet.

d. Show that

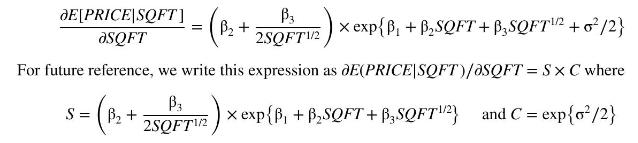
Correspondingly, we let \(\hat{S}\) and \(\hat{C}\) denote estimates for \(S\) and \(C\) obtained by replacing unknown parameters by their estimates.

e. Estimate \(\partial E(P R I C E \mid S Q F T) / \partial S Q F T=S \times C\) for houses with (i) 1500 square feet, (ii) 3000 square feet, and (iii) 4500 square feet.

f. Finding the asymptotic standard errors for the estimates in (e) is tricky because of the product \(\hat{S} \times \hat{C}\). To avoid such trickiness, find the standard errors for \(\hat{S}\) for each type of house in (e).

g. For each type of house, and a \(5 \%\) significance level, use the estimates from (e) and the standard errors from (f) to test the hypotheses

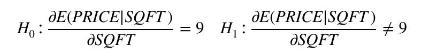
What do you conclude?

h. To get the "correct" standard errors for \(\hat{S} \times \hat{C}\), we proceed as follows. First, given \(\operatorname{var}\left(\hat{\sigma}^{2}\right)=2 \sigma^{4} /(N-K)\), find an estimate for \(\operatorname{var}(\hat{C})\). It can be shown that \(\hat{S}\) and \(\hat{C}\) are independent. Using results on the product of independent random variables, an estimator for the variance of \(\hat{S} \times \hat{C}\) is

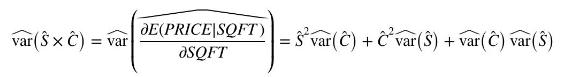
Use this result to find standard errors for \(\hat{S} \times \hat{C}\). How do they compare with the standard errors obtained in (f)? Are they likely to change the outcomes of the hypothesis tests in (g)?

Transcribed Image Text:

In(PRICE) = B + BSQFT + BSQFT/ + e