This exercise shows that in a simple regression model, adding a dummy variable for missing data on the explanatory variable produces a consistent estimator of the slope coefficient if the “missingness” is unrelated to both the unobservable and observable factors affecting y. Let m be a variable such that m = 1 if we do not observe x and m 5 0 if we observe x. We assume that y is always observed. The population model is

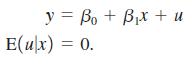
(i) Provide an interpretation of the stronger assumption

E(u|x,m) = 0.

In particular, what kind of missing data schemes would cause this assumption to fail?

(ii) Show that we can always write

(iii) Let (x_i, y_i, m_i): i = 1, . . . , n be random draws from the population, where xi is missing when mi = 1. Explain the nature of the variable z_i = (1 – m_i)x_i. In particular, what does this variable equal when xi is missing?

(iv) Let r = P(m = 1) and assume that m and x are independent. Show that

Cov[(1 – m)x,mx] = – ρ(1 – ρ)µ_x,

where µ_x = E(x). What does this imply about estimating β₁ from the regression y_i on z_i, i = 1, . . . , n?

(v) If m and x are independent, it can be shown that

mx = δ₀ + δ₁m + v,

where v is uncorrelated with m and z = (1 – m)x. Explain why this makes m a suitable proxy variable for mx. What does this mean about the coefficient on z_i in the regression

y_i on z_i, m_i, i = 1, . . . , n?

(vi) Suppose for a population of children, y is a standardized test score, obtained from school records, and x is family income, which is reported voluntarily by families (and so some families do not report their income). Is it realistic to assume m and x are independent? Explain.

Transcribed Image Text:

y = E(ux) = 0. Bo + Bx + u