Suppose that log(y0 follows a linear model with a linear form of heteroskedasticity. We write this as

so that, conditional on x, u has a normal distribution with mean (and median) zero but with variance h(x) that depends on x. Because Med(u|x) = 0, equation (9.48) holds: Med(y|0x) = exp(β₀ + xβ).Further, using an extension of the result from Chapter 6, it can be shown that

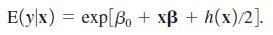
(i) Given that h(x) can be any positive function, is it possible to conclude δE(y|x)δx_j is the same sign as β_j?

(ii) Suppose h(x) = δ₀ + xδ (and ignore the problem that linear functions are not necessarily always positive). Show that a particular variable, say x₁, can have a negative effect on Med(y|x) but a positive effect on E(y|x).

(iii) Consider the case covered in Section 6-4, in which h(x) = σ². How would you predict y using an estimate of E(y|x)? How would you predict y using an estimate of Med(y|x)? Which prediction is always larger?

Transcribed Image Text:

log(y) = Bo + xB + u ulx - Normal[0,h(x)],