The point of this exercise is to show that tests for functional form cannot be relied on as a general test for omitted variables. Suppose that, conditional on the explanatory variables x₁ and x₂, a linear model relating y to x₁ and x₂ satisfies the Gauss-Markov assumptions:

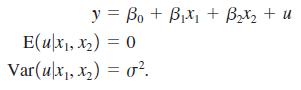
To make the question interesting, assume β₂ ¹ 0.

Suppose further that x₂ has a simple linear relationship with x₁:

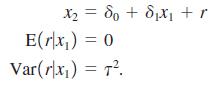
(i) Show that

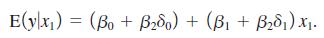
Under random sampling, what is the probability limit of the OLS estimator from the simple regression of y on x₁? Is the simple regression estimator generally consistent for β₁?

(ii) If you run the regression of y on x₁, x²₁, what will be the probability limit of the OLS estimator of the coefficient on x²₁? Explain.

(iii) Using substitution, show that we can write

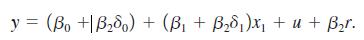
It can be shown that, if we define

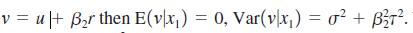
What consequences does this have for the t statistic on x²₁ from the regression in part (ii)?

(iv) What do you conclude about adding a nonlinear function of x₁—in particular, x²₁ —in an attempt to detect omission of x₂?

Transcribed Image Text:

y = Bo + Bx, + Bx2 + u E(ulx1, x2) = 0 Var(ulx,, x,) = 0?.