Consider a wheel with \(n\) sectors. If the wheel pointer lands on sector \(i\), the payoff obtained is \(r_{i}\) for every unit bet on that sector. The chance of landing on sector \(i\) is \(p_{i}, i=1,2, \ldots, n\). Let \(\alpha_{i}\) be the fraction of one's capital bet on sector \(i\). We require \(\sum_{i=1}^{n} \alpha_{i} \leq 1\) and \(\alpha_{i} \geq 0\) for \(i=1,2, \ldots, n\).

(a) Show that the optimal growth strategy is obtained by solving

\[\max \sum_{j=1}^{n} p_{j} \ln \left(r_{j} \alpha_{j}+1-\sum_{i=1}^{n} \alpha_{i}\right)\]

(b) Assuming that \(\alpha_{i}>0\) for all \(i=1,2, \ldots, n\), show that the optimal values must satisfy

\[\frac{p_{k} r_{k}}{r_{k} \alpha_{k}+1-\sum_{i=1}^{n} \alpha_{i}}-\sum_{j=1}^{n} \frac{p_{j}}{r_{j} \alpha_{j}+1-\sum_{i=1}^{n} \alpha_{i}}=0\]

for all \(k=1,2, \ldots, n\).

(c) Assume that \(\sum_{i=1}^{n} 1 / r_{i}=1\). Show that in this case a solution is \(\alpha_{i}=p_{j}\) for \(i=\) \(1,2, \ldots, n\).

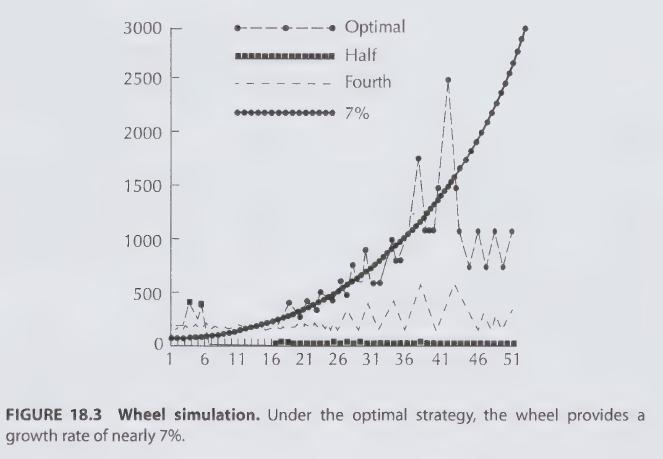
(d) For the wheel given in Example 18.5, find the optimal solution and determine the corresponding optimal growth rate.

Example

Transcribed Image Text:

Example 18.5 (The investment wheel) Let us compute the full optimal strategy for the investment wheel allowing for the possibility of investing on all sectors. For a strategy (a1, a2, 3) we find the results as follows: 1. If 1 occurs, R=1+2--3. 2. If 2 occurs, R = 1-1+-3. 3. If 3 occurs, R = 1-1-+53. To maximize the expected logarithm of this return structure, we maximize m=ln(1+21-2-3)+ln(1-1 +2-3)+ln(1-1-+53). If we assume that the solution has a; > 0 for each i = 1,2,3, we can find the solution by setting the derivatives with respect to each a; equal to zero. This gives the equations 2 1 1 3(1-1 +2-3) 6(1 1 2+53) 0 2(1+2-2-3) 1 1 1 + =0 2(1+21-a2-3) 3(1-1+-3) 6(1-1-a2+503) 1 1 5 + 0. 2(1+2a1-a2-3) 3(1-1+a2-03) 6(1-1 2+503)