Suppose that it is desired to estimate the expected value of a random variable \(x\). (This random variable might be the discounted terminal value of a call option on a stock that is following a risk-neutral random process; then the expected value is the value of the option.) One way to do the estimation is to generate numerous samples of \(x\), according to its probability distribution, and then take the average of the results. A difficulty with this method is that it may take a very large number of samples to obtain satisfactory results. The process can be speeded up somewhat by the use of an additional random variable \(y\) called a control variate. The control variate must be correlated with \(x\), and its expected value must be known. For example, if \(x\) is the terminal value of a call with a down and out feature, we might choose \(y\) to be the terminal value of a similar call without the down and out feature. We can determine the value of \(\mathrm{E}(y)=\bar{y}\) by direct methods such as the Black-Scholes formula or a binomial lattice. But we do expect that if the stock should happen to end high on a particular simulation trial, the value of both \(x\) and \(y\) will be relatively high as well. Hence the two variables are correlated.

The estimate \(\hat{x}\) of \(\mathrm{E}(x)\) is made with the formula

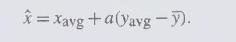
Sometimes a small value of \(a\) is selected arbitrarily. However, an optimal value of \(a\) can be estimated as well. Find the value of \(a\) that minimizes the variance of \(\hat{x}\). (The result will depend on certain variances and covariances.)

Transcribed Image Text:

Xavg+a(yavg).