Suppose there is a master space $\Omega$ of payoff elements (of finite dimension), of which those in the market are in the subspace $\mathcal{M}$.

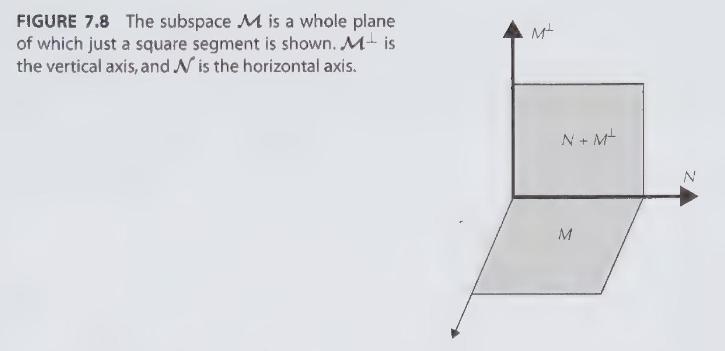
We may write $\Omega=\mathcal{M}+\mathcal{M}^{\perp}$, where $\mathcal{M}^{\perp}$ is the set of all elements orthogonal to $\mathcal{M}$. That is, any element $x \in \Omega$ can be expressed as $x=m+m^{\perp}$ with $m \in \mathcal{M}$ and $m^{\perp} \in \mathcal{M}^{\perp}$. Let $\mathcal{N}$ be a subspace of $\mathcal{M}$, and consider all payoffs in the subspace $\mathcal{X}=\mathcal{N}+\mathcal{M}^{\perp}$ in $\Omega$. (See Figure 7.8 for $\Omega$ equal to three-dimensional space.) Show that for an $x \in \mathcal{X}$, the projection of $x$ onto $\mathcal{M}$ is equal to the projection of $x$ onto $\mathcal{N}$. Likewise, a most correlated asset to $x$ is in $\mathcal{N}$. Hence, to find the projection price of $x$, it is only necessary to consider its relation to market payoffs in its local $\mathcal{N}$.

Transcribed Image Text:

FIGURE 7.8 The subspace M is a whole plane of which just a square segment is shown. M- is the vertical axis, and N is the horizontal axis. Mt N+M+ M