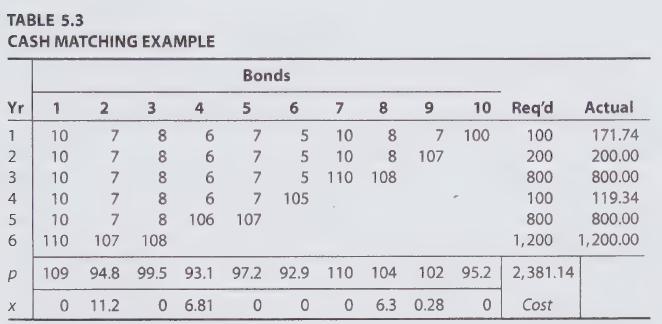
The cash matching and other problems can be conveniently represented in matrix form. Suppose there are $m$ bonds. We define for each bond $j$ its associated yearly cash flow stream (column) vector $\mathbf{c}_{j}$, which is $n$-dimensional. The yearly obligations are likewise represented by the $n$-dimensional vector $\mathbf{y}$. We can stack the $\mathbf{c}_{j}$ vectors side by side to form the columns of a bond matrix $\boldsymbol{C}$. Finally we let $\mathbf{p}$ and $\mathbf{x}$ be $\boldsymbol{m}$-dimensional column vectors. The cash matching problem can be expressed as

(a) Identify $\mathbf{C}, \mathbf{y}, \mathbf{p}$, and $\mathbf{x}$ in Table 5.3.

(b) Show that if all bonds are priced according to a common term structure of interest rates, there is a vector $\mathbf{v}$ satisfying

\[\mathbf{C}^{T} \mathbf{v}=\mathbf{p}\]

What are the components of $\mathbf{v}$ ?

(c) Suppose $\mathbf{b}$ is a vector whose components represent obligations in each period. Show that a portfolio $\mathbf{x}$ meeting these obligations exactly satisfies

\[\mathbf{C x}=\mathbf{b}\]

(d) With $\mathbf{x}$ and $\mathbf{v}$ defined as before, show that the price of the portfolio $\mathbf{x}$ is $\mathbf{v}^{T} \mathbf{b}$. Interpret this result.

Transcribed Image Text:

TABLE 5.3 CASH MATCHING EXAMPLE Bonds Yr 1 2 3 4 5 10 6 7 8 9 10 Req'd Actual 1 10 7 8 2345 10 7 8 66 7 5 10 8 7 100 100 171.74 7 5 10 8 107 200 200.00 10 7 8 6 7 5 110 108 800 800.00 4 10 7 8 6 7 105 100 119.34 5 10 7 8 106 107 800 800.00 6 110 107 108 1,200 1,200.00 P 109 94.8 99.5 93.1 97.2 92.9 110 104 102 95.2 2,381.14 X 0 11.2 0 6.81 0 0 0 6.3 0.28 0 Cost