In Example 19‐17, N(d₁) was 0.4785; therefore, to hedge a 1,000 share portfolio, the investor should write 21 call options [(1/0.4785) 1,000 2,089.86 individual options or about 21 contracts]. A $1 increase in the price of the stock should produce approximately a $0.4785 change in the price of the option. The loss on the call options written is 2,100 × $0.4785 = $1,004.85, which is approximately offset by the $1 per‐share gain on the 1,000 shares. A perfectly hedged position leaves total wealth unchanged.

Example 19‐17

The following is an example of the use of the Black–Scholes option pricing formula: Assume

S = $40

E = $45

r = 0.10

t = 0.5 (6 months)

σ = 0.45

Step 1: Solve for d₁.

Step 2: Use a cumulative probability distribution table to find the value of N (d₁).

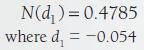
Step 3: Find d₂.

Step 4: Find N (d₂).

Step 5: Solve for C.

Transcribed Image Text:

d₁ In(40/45) + [0.10+0.5(0.45)²10.5 0.45 [(0.5) ¹/2] -0.1178 +0.1006 0.3182 = -0.054