Consider the problem of finding the least expensive routes to all cities in a network from a given starting point. For example, in the network shown on the map on page 733, the least expensive route from Pendleton to Peoria has cost 8 (going through Pierre and Pueblo). The following helper class expresses the distance to another city:

public class DistanceTo implements Comparable
{
private String target;
private int distance;
public DistanceTo(String city, int dist) { target = city; distance = dist; }
public String getTarget() { return target; }
public int getDistance() { return distance; }
public int compareTo(DistanceTo other) { return distance - other.distance; }
}

All direct connections between cities are stored in a Map>.
The algorithm now proceeds as follows:

Let from be the starting point.
Add DistanceTo(from, 0) to a priority queue.
Construct a map shortestKnownDistance from city names to distances.
While the priority queue is not empty
Get its smallest element.
If its target is not a key in shortestKnownDistance
Let d be the distance to that target.
Put (target, d) into shortestKnownDistance.
For all cities c that have a direct connection from target
Add DistanceTo(c, d + distance from target to c) to the priority queue.

When the algorithm has finished, shortestKnownDistance contains the shortest distance from the starting point to all reachable targets.

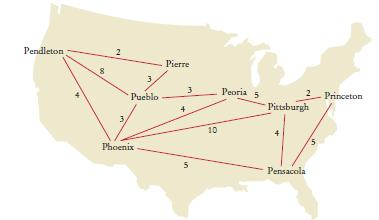
Your task is to write a program that implements this algorithm. Your program should read in lines of the form city1 city2 distance. The starting point is the first city in the first line. Print the shortest distances to all other cities.

Pendleton Pierre Pueblo Peoria 5 Princeton Pittsburgh 10 Phoenix 5 Pensacola in