Projectile flight. Suppose a cannonball is propelled straight into the air with a starting velocity v 0
Question:
Projectile flight. Suppose a cannonball is propelled straight into the air with a starting velocity v0. Any calculus book will state that the position of the ball after t seconds
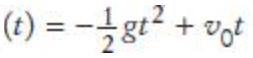where g = 9.81 m/s2 is the gravitational force of the earth. No calculus textbook ever mentions why someone would want to carry out such an obviously dangerous experiment, so we will do it in the safety of the computer. In fact, we will confirm the theorem from calculus by a simulation. In our simulation, we will consider how the ball moves in very short time intervals Δt. In a short time interval the velocity v is nearly constant, and we can compute the distance the ball moves as Δs = vΔt. In our program, we will simply set final double DELTA_T = 0.01; and update the position by s = s + v * DELTA_T;
The velocity changes constantly—in fact, it is reduced by the gravitational force of the earth. In a short time interval, Δv = –gΔt, we must keep the velocity updated as v = v - g * DELTA_T; In the next iteration the new velocity is used to update the distance. Now run the simulation until the cannonball falls back to the earth. Get the initial velocity as an input (100 m/s is a good value). Update the position and velocity 100 times per second, but print out the position only every full second. Also printout the values from the exact formula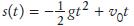 
for comparison.
Note: You may wonder whether there is a benefit to this simulation when an exact formula is available. Well, the formula from the calculus book is not exact. Actually, the gravitational force diminishes the farther the cannonball is away from the surface of the earth. This complicates the algebra sufficiently that it is not possible to give an exact formula for the actual motion, but the computer simulation can simply be extended to apply a variable gravitational force. For cannonballs, the calculus-book formula is actually good enough, but computers are necessary to compute accurate trajectories for higher-flying objects such as ballistic missiles.
Step by Step Answer:
Heres a Java program that simulates the flight of a cannonball public class Cannonball public static ...View the full answer
