Rewrite Exercise to obtain imaginary roots if the determinant is less than 0 using the?Complex?class in Exercise.

Question:

Rewrite Exercise to obtain imaginary roots if the determinant is less than 0 using the?Complex?class in Exercise. Here are some sample runs.

(Algebra: solve quadratic equations) The two roots of a quadratic equation?ax2 +?bx?+?c?= 0 can be obtained using the following formula:

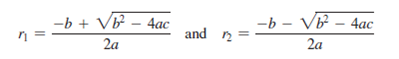
b2 - 4ac?is called the discriminant of the quadratic equation. If it is positive, the equation has two real roots. If it is zero, the equation has one root. If it is negative, the equation has no real roots.

Write a program that prompts the user to enter values for?a,?b, and?c?and displays the result based on the discriminant. If the discriminant is positive, display two roots. If the discriminant is?0, display one root. Otherwise, display ?The equation has no real roots?.

Note that you can use Math.pow(x, 0.5) to compute 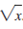. Here are some sample runs.

A complex number is a number in the form a + bi, where a and b are real numbers and i is 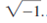. The numbers?a?and?b?are known as the real part and imaginary part of the complex number, respectively. You can perform addition, subtraction, multiplication, and division for complex numbers using the following formulas:

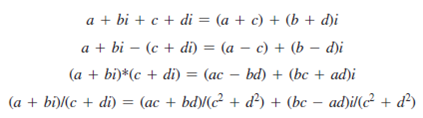
You can also obtain the absolute value for a complex number using the following

formula:

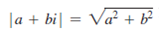
(A complex number can be interpreted as a point on a plane by identifying the (a,b) values as the coordinates of the point. The absolute value of the complex number corresponds to the distance of the point to the origin, as shown in Figure.)

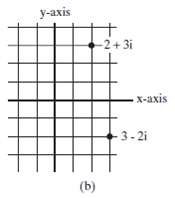
Design a class named?Complex?for representing complex numbers and the methods?add,?subtract,?multiply,?divide, and?abs?for performing complexnumber operations, and override?toString?method for returning a string representation for a complex number. The?toString?method returns?(a + bi)?as a string. If?b?is?0, it simply returns?a. Your?Complex?class should also implement the?Cloneable?interface.

Provide three constructors?Complex(a, b),?Complex(a), and?Complex().?Complex()?creates a?Complex?object for number?0?and?Complex(a)?creates a?Complex?object with?0?for?b. Also provide the?getRealPart()?and?getImaginaryPart()?methods for returning the real and imaginary part of the complex number, respectively.

Write a test program that prompts the user to enter two complex numbers and displays the result of their addition, subtraction, multiplication, division, and absolute value. Here is a sample run: