4.28 Suppose we wish to test the noise alone hypothesis H0 : xt = nt against the signal-plus-noise hypothesis H1 : xt = st + nt, where st and nt are uncorrelated zero-mean stationary processes with spectra fs(ω) and fn(ω). Suppose that we want the test over a band of L = 2m + 1 frequencies of the form ωj:n + k, for k = 0,±1,±2, . . . ,±m near some fixed frequency ω. Assume that both the signal and noise spectra are approximately constant over the interval.

(a) Prove the approximate likelihood-based test statistic for testing H0 against H1 is proportional to

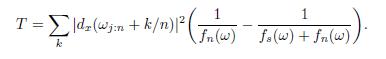
(b) Find the approximate distributions of T under H0 and H1.

(c) Define the false alarm and signal detection probabilities as PF = P{T > K| H0} and Pd = P{T > k| H1}, respectively. Express these probabilities in terms of the signal-to-noise ratio fs(ω)/fn(ω) and appropriate chi-squared integrals.

Transcribed Image Text:

1 T = \dz (wijn + k/n) | (Jn (w) (Fn (w) - Fo(w) + (w)). fn(w) fs(w)+fn(w),