A is an m x n matrix with a singular value decomposition A = UV T ,

A is an m x n matrix with a singular value decomposition A = UΣV^T, where U is an m x m orthogonal matrix, Σ is an m x n "diagonal" matrix with r positive entries and no negative entries, and V is an n x n orthogonal matrix. Justify each answer.

Using the notation of Exercise 23, show that A^Tu_j = σ_jv_j for ≤ j ≤ r = rank A.

Data From Exercise 23

A is an m x n matrix with a singular value decomposition A = UΣV^T, where U is an m x m orthogonal matrix, Σ is an m x n "diagonal" matrix with r positive entries and no negative entries, and V is an n x n orthogonal matrix. Justify each answer.

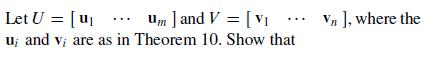Let U = [u_1.......u_m] and V = [v_{1 .......} u_n] ; where the u_i and v_i are as in Theorem 10. Show that 

Transcribed Image Text:

Let U = [u₁ Um ] and V = [VI u; and v; are as in Theorem 10. Show that Vn ], where the