Another estimate can be made for an eigenvalue when an approximate eigenvector is available. Observe that if
Question:
Another estimate can be made for an eigenvalue when an approximate eigenvector is available. Observe that if Ax = λx, then xTAX = xT(λx) = λ(xTx), and the Rayleigh quotient
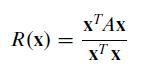
equals λ. If x is close to an eigenvector for λ, then this quotient is close to λ. When A is a symmetric matrix (AT = A), the Rayleigh quotient R(xk) = (xTk Axk)/(xTk xk) will have roughly twice as many digits of accuracy as the scaling factor μk in the power method. Verify this increased accuracy by computing μk and R(xk) for k = 1,...,4.
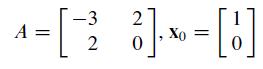
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Linear Algebra And Its Applications
ISBN: 9781292351216
6th Global Edition
Authors: David Lay, Steven Lay, Judi McDonald
Question Posted:





