Example 2 in Section 4.8 displayed a low-pass linear filter that changed a signal {y k }
Question:
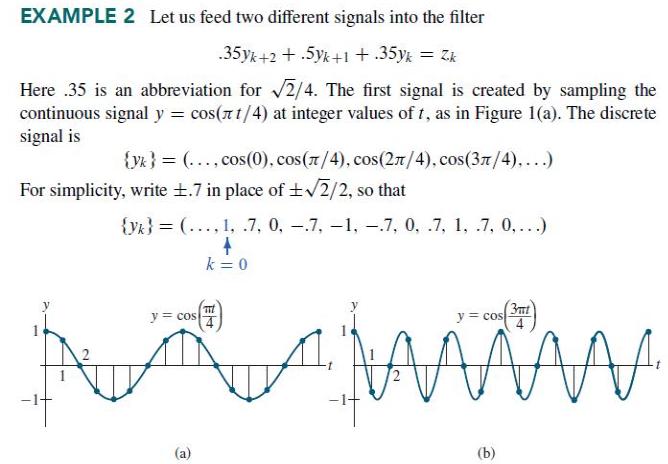
Example 2 in Section 4.8 displayed a low-pass linear filter that changed a signal {yk} into {yk+1} and changed a higher-frequency signal {ωk} into the zero signal, where yk = cos(πk/4) and (ωk) = cos(3πk/4). The following calculations will design a filter with approximately those properties. The filter equation is
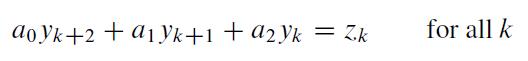
Write an equation Ax = b, where A is a 16 x 3 matrix formed from the two coefficient matrices above and where b in R16 is formed from the two right sides of the equations. Find a0, a1, and a2 given by the least-squares solution of Ax = b. (The .7 in the data above was used as an approximation for √2/2, to illustrate how a typical computation in an applied problem might proceed. If .707 were used instead, the resulting filter coefficients would agree to at least seven decimal places with √2/4; 1/2, and √2/4, the values produced by exact arithmetic calculations.)
Data From Example 2 in Section 4.8
Step by Step Answer:
To find the leastsquares solution for the filter coefficients a0 a1 and a2 we need to construct the matrix equation Ax b where A is a 16 x 3 matrix fo...View the full answer
Linear Algebra And Its Applications
ISBN: 9781292351216
6th Global Edition
Authors: David Lay, Steven Lay, Judi McDonald
