Let B = {1, cost, cos² t,..., cos⁶ t and C = {1, cos t, cos 2t,...,cos 6t}. Assume the following trigonometric identities (see Exercise 45 in Section 4.1).

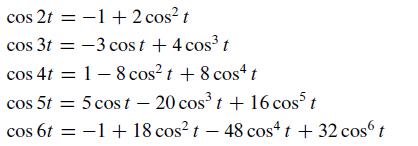
Let H be the subspace of functions spanned by the functions in B. 

a. Write the B-coordinate vectors of the vectors in C, and use them to show that C is a linearly independent set in H. 

b. Explain why C is a basis for H.

Data from in Exercise 45

The vector space H = Span {1, cos² t, cos⁴ t, cos⁶ t contains at least two interesting functions that will be used in a later exercise:

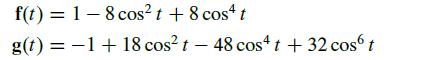
Study the graph of f for 0 ≤ t ≤ 2π, and guess a simple formula for f(t). Verify your conjecture by graphing the difference between 1 + f(t) and your formula for f(t). (Hope- fully, you will see the constant function 1.) Repeat for g.

Transcribed Image Text:

cos 2t = cos 3t = cos 4t cos 5t = = 1 + 2 cos² t 3 cost + 4 cos³ t 18 cos² t + 8 cost 5 cost - 20 cos³ t + 16 cos t cos 6t= 1 + 18 cos² t - 48 cost +32 cost -