Let x(t) be the B-spline in Exercise 2, with control points p₀, p₁, p₂, and p₃.
a. Compute the tangent vector x'(t) and determine how the derivatives x'(0) and x'(1) are related to the control points. Give geometric descriptions of the directions of these angent vectors. Explore what happens when both x'(0) and x'(1) equal 0. Justify your assertions.
b. Compute the second derivative x"(t) and determine how x"(0) and x"(1) are related to the control points. Draw a figure based on Figure 10, and construct a line segment that points in the direction of x"(1).

Data From Exercise 2

The parametric vector form of a B-spline curve was defined in the Practice Problems as

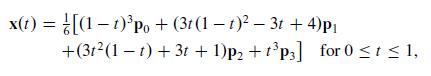
where p₀, p₁, p₂, and p₃ are the control points.

a. Show that for 0 ≤ t ≤ 1(x)t / is in the convex hull of the control points.
b. Suppose that a B-spline curve x(t) is translated to x(t) + b (as in Exercise 1). Show that this new curve is again a B-spline.

Data From Exercise 1

Suppose a Bézier curve is translated to x(t) + b. That is, for 0 ≤ t ≤ 1, the new curve is

Show that this new curve is again a Bézier curve.

Transcribed Image Text:

FIGURE 10 A B-spline segment and a Bézier curve.