Show how the axioms for a vector space V can be used to prove the elementary properties described after the definition of a vector space. Fill in the blanks with the appropriate axiom numbers. Because of Axiom 2, Axioms 4 and 5 imply, respectively, that 0 + u = u and -u + u = 0 for all u.

Complete the following proof that -u is the unique vector in V such that u + (-u) = 0. Suppose that w satisfies u + w = 0. Adding -u to both sides, we have

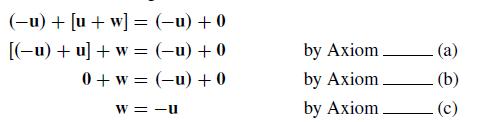
Transcribed Image Text:

(-u) + [u+w] = (-u) + 0 [(-u) + u] + w = (-u) +0 0+w= (-u) + 0 W=-U by Axiom by Axiom. by Axiom (b) (c)