Explore one approach to the problem of finding the projection of a vector onto a plane. As Figure 1.69 shows, if P is a plane through the origin in R³with normal vector n, and v is a vector in R³, then p = proj_P(v) is a vector in P such that v - cn = p for some scalar c.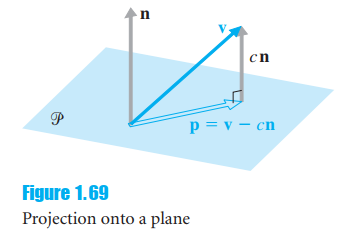

Using the fact that n is orthogonal to every vector in P (and hence to p), solve for c and thereby find an expression for p in terms of v and n.

cn p = v cn Figure 1.69 Projection onto a plane