Explore one approach to the problem of finding the projection of a vector onto a plane. As Figure 1.69 shows, if P is a plane through the origin in R³with normal vector n, and v is a vector in R³, then p = proj_P(v) is a vector in P such that v - cn = p for some scalar c.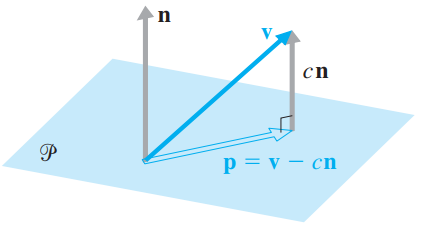

Use the method of Exercise 43 to find the projection of  onto the planes with the following equations: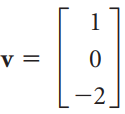

(a) x + y + z = 0 

(b) 3x - y + z = 0

(c) x - 2z = 0

(d) 2x - 3y + z = 0

cn p = v cn -2,