The Fibonacci recurrence f_n= f_n-1+ f_n-2has the associated matrix equation x_n= Ax_n-1, where

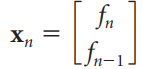
and 

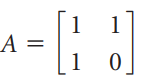
(a) With f₀ = 0 and f₁ = 1, use mathematical induction to prove that

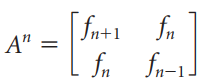
for all n ‰¥ 1.
(b) Using part (a), prove that

f_n+1f_n-1 - f²_n = (-1)ⁿ

for all n 1. [This is called Cassini€™s Identity, after the astronomer Giovanni Domenico Cassini (1625€“1712). Cassini was born in Italy but, on the invitation of Louis XIV, moved in 1669 to France, where he became director of the Paris Observatory. He became a French citizen and adopted the French version of his name: Jean-Dominique Cassini. Mathematics was one of his many interests other than astronomy. Cassini€™s Identity was published in 1680 in a paper submitted to the Royal Academy of Sciences in Paris.]
(c) An 8  8 checkerboard can be dissected as shown in Figure 4.29(a) and the pieces reassembled to form the 5  13 rectangle in Figure 4.29(b).

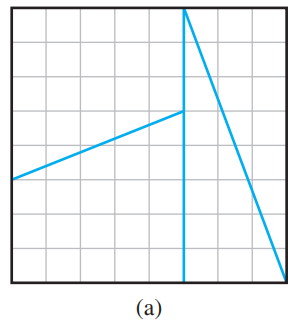
The area of the square is 64 square units, but the rectangle€™s area is 65 square units! Where did the extra square come from?

fn LJn-1J A =