The process of adding rational functions (ratios of polynomials) by placing them over a common denominator is the analogue of adding rational numbers. The reverse process of taking a rational function apart by writing it as a sum of simpler rational functions is useful in several areas of mathematics; for example, it arises in calculus when we need to integrate a rational function and in discrete mathematics when we use generating functions to solve recurrence relations. The decomposition of a rational function as a sum of partial fractions leads to a system of linear equations. Find the partial fraction decomposition of the given form.

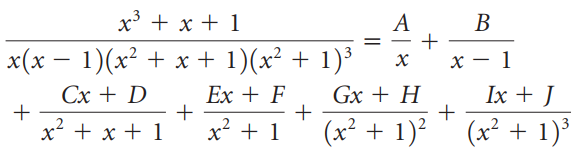
Following are two useful formulas for the sums of powers of consecutive natural numbers: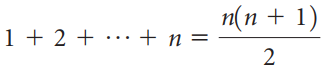

and 

The validity of these formulas for all values of n 1 (or even n 0) can be established using mathematical induction (see Appendix B). One way to make an educated guess as to what the formulas are, though, is to observe that we can rewrite the two formulas above as 

_1/2n² + _1/2n and _1/3n³ + _1/2n² + _1/6n

respectively. This leads to the conjecture that the sum of pth powers of the first n natural numbers is a polynomial of degree p + 1 in the variable n.

Transcribed Image Text:

х3 + x+1 B x(х — 1)(x? + х + 1)(x? + 1)? х х Сх + D Gx + H Ix + J Ex + F (x² + 1) х + 1 х* + x+1 (х? + 1)? п(п + 1) 1 + 2 + · + n =