A light, stiff, strong tie (Fig. E8.1). A tie, of length \(L\) loaded in tension, is to support a load \(F\), at minimum weight without failing (implying a constraint on strength) or extending elastically by more than \(\delta\) (implying a constraint on stiffness, \(F / \delta\) ). The table summarizes the requirements.

a. Follow the method of this chapter to establish two performance equations for the mass, one for each constraint, from which two material indices and one coupling equation linking them are derived. Show that the two indices and the coupling equation are (in order):
\[M_{1}=\frac{ho}{E} \quad \text { and } \quad M_{2}=\frac{ho}{\sigma_{y}} \quad \text { and } \quad\left(\frac{ho}{\sigma_{y}}\right)=\frac{L}{\delta}\left(\frac{ho}{E}\right)\]

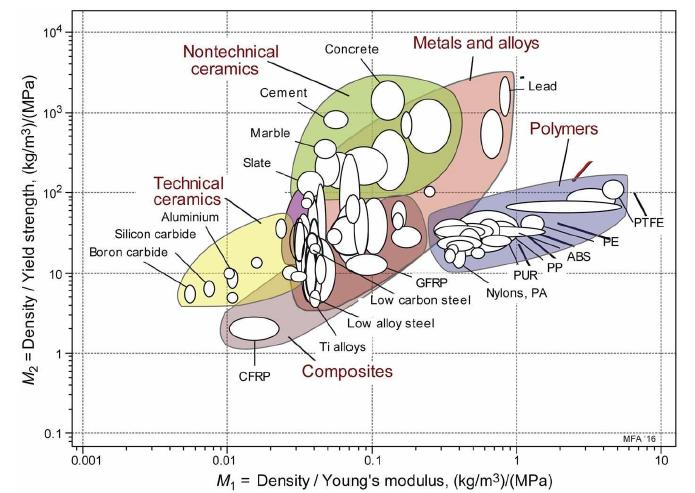
b. Use these and the material chart of Fig. E8.2, which has the indices as axes, to identify candidate materials for the tie (1) when the permitted elastic strain is \(\delta\) \(/ L=10^{-3}\) and (2) when \(\delta / L=10^{-2}\).

Data From Fig, 8.1

Data From Fig, 8.2

Function Constraints Objective Free variables Tie rod Must not fail by yielding under force F Must have specified stiffness, F/8 Length Land axial load F specified Minimize mass m Section area A Choice of material