A system is shown in the following Fig.11. The bar \(A B\) is assumed to be rigid and weightless.

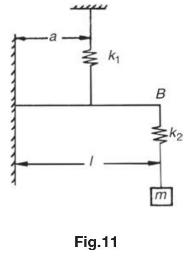
The natural frequency of vibration of the system is given by

(a) \(f_{n}=\frac{1}{2 \pi} \frac{\sqrt{k_{1} k_{2}\left(\frac{a}{\ell}\right)^{2}}}{m\left[k_{2}+\left(\frac{a}{\ell}\right)^{2} k_{1}\right]}\)

(b) \(f_{n}=\frac{1}{2 \pi} \frac{\sqrt{k_{1} k_{2}}}{m\left(k_{1}+k_{2}\right)}\)

(c) \(f_{n}=\frac{1}{2 \pi} \frac{\sqrt{k_{1}}}{m k_{2}}\)

(d) \(f_{n}=\frac{1}{2 \pi} \frac{\sqrt{k_{1}+k_{2}}}{m k_{1} k_{2}}\).

a Fig.11 B m