Start each of the four parts of this problem by listing the function, the objective and the constraints. You will need the equations for the deflection of a cantilever beam with a square cross-section \(t \times t\), given in Appendix B, Section B3. The two that matter are that for the deflection \(\delta\) of a beam of length \(L\) under an end load F:

a. Show that the best material for a cantilever beam of given length \(L\) and given (i.e., fixed) square cross-section \((t \times t)\), that will deflect least under a given end load \(F\), is that with the largest value of the index \(M=E\), where \(E\) is Young's modulus (neglect self-weight) Fig. E4.12A.

b. Show that the best material choice for a cantilever beam of given length \(L\) and with a given section \((t \times t)\) that will deflect least under its own selfweight is that with the largest value of \(M=E / ho\), where \(ho\) is the density Fig. E4.12B.

c. Show that the material index for the lightest cantilever beam of length \(L\) and square section (not given, i.e., the area is a free variable) that will not deflect by more than \(\delta\) under its own weight is \(M=E / ho^{2}\) Fig. E4.12C.

d. Show that the lightest cantilever beam of length \(L\) and square section (area free) that will not deflect by more than \(\delta\) under an end load \(F\) is that made of the material with the largest value of \(M=E^{1 / 2} / ho\) (neglect self-weight) Fig. E4.12D.

Data From Appendix B3

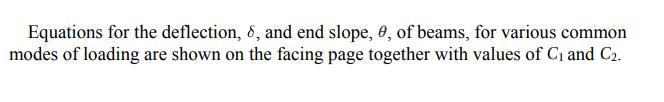
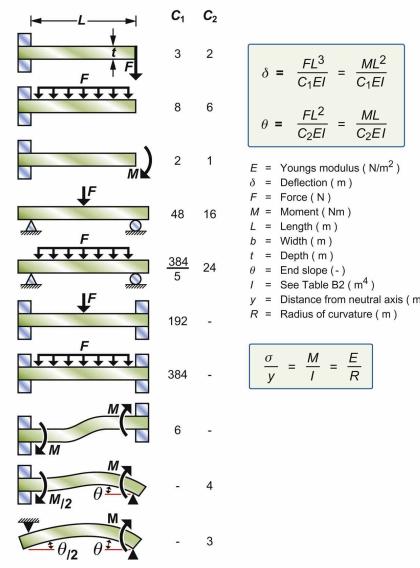
Fig. E4.12C

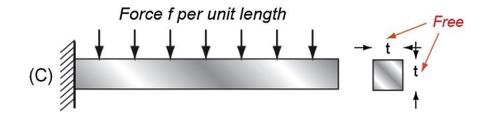
Fig. E4.12B

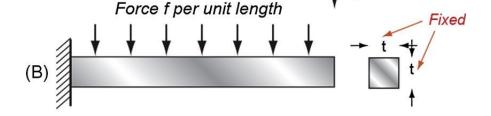
Fig. E4.12D

Transcribed Image Text:

B.3 Elastic Bending of Beams When a beam is loaded by a force F or moments M, the initially straight axis is deformed into a curve. If the beam is uniform in section and properties, long in relation to its depth and nowhere stressed beyond the elastic limit, the deflection 8, and the angle of rotation, 0, can be calculated using elastic beam theory (see Further Reading in Section B.17). The basic differential equation describing the curvature of the beam at a point x along its length is = M where y is the lateral deflection, and M is the bending moment at the point x on the beam. E is Young's modulus and I is the second moment of area (Section B.2). When M is constant this becomes *--*) M=E(