The elastic deflection at fracture (the 'resilience') of an elastic-brittle solid is proportional to the failure strain, \(\varepsilon_{f r}=\sigma_{f r} / E\), where \(\sigma_{f r}\) is the stress that will cause a crack to propagate:

\[\sigma_{f \mathrm{r}}=\frac{K_{1 c}}{\sqrt{\pi c}}\]
Here \(K_{1 c}\) is the fracture toughness and \(c\) is the length of the longest crack the materials may contain. Thus \[\varepsilon_{f r}=\frac{1}{\sqrt{\pi c}}\left(\frac{K_{1 c}}{E}\right)\]
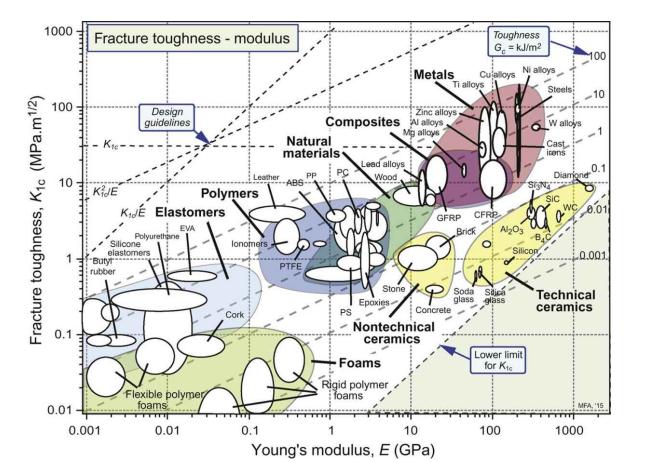
Materials that can deflect elastically without fracturing are therefore those with large values of \(K_{1 c} / E\). Use the \(K_{l c}-E\) chart of Fig. 3.7 to identify the class of materials with \(K_{1 c}>1 \mathrm{MPa} \mathrm{m}^{1 / 2}\) and high values of \(K_{1 c} / E\). Position the \(K_{1 c} / E\) criterion such that all metals are excluded.

Fig. 3.7

Transcribed Image Text:

1000 Fracture toughness - modulus 100 Design guidelines Fracture toughness, Kc (MPa.m1/2) 10 Metals Zinc alloys Composites Al alloys, Mg alloys Natural materials Lead alloys Leather PP PC Wood ABS- KJE Polymers KJE Elastomers EVA Polyurethane Silicone Ionomers elastomers Buty PTFE rubber 0.1 0.01 Prietaire polymer foams 0.001 Cork 0.01 0.1 Toughness G = kJ/m Cu alloys Ni alloys Steels Ti alloys OW alloys 100 10 Cast icens 0.1 Diamond SIGN SIC WC 0001 GFRP CFRP Brick Al2O3 Silicon 0.001 Stone Soda Saica Epoxies- Concrete Technical ceramics Nontechnical ceramics Foams Rigid polymer foams Lower limit for K MFA 15 10 100 1000 Young's modulus, E (GPa)