Consider the following economy. Desired consumption (quad C^{d}=325+0.5(Y-T)) (-500 r). Desired investment (I^{d}=200-500 r). Government purchases (quad
Question:
Consider the following economy.
Desired consumption \(\quad C^{d}=325+0.5(Y-T)\) \(-500 r\).
Desired investment \(I^{d}=200-500 r\).
Government purchases \(\quad G=150\).
Taxes \(T=150\).
Real money demand \(L=0.5 Y-1000 r\).
Money supply \(M=6000\).
Full-employment output \(\bar{Y}=1000\).
Note that the expected rate of inflation is assumed to equal zero so that money demand depends directly on the real interest rate, which equals the nominal interest rate.
a. Calculate the full-employment values of the real interest rate, the price level, consumption, and investment.
b. What are the values of \(\alpha_{I S}, \beta_{I S}, \alpha_{L M}, \beta_{L M}\), and \(\ell_{r}\) for this economy?
c. Suppose that the price level is fixed at \(P_{s r}=15\). What are the short-run equilibrium values of output and the real interest rate?
d. With the price level still fixed at \(P_{s r}=15\), suppose that government purchases increase from \(G=150\) to \(G=250\). What are the new values of \(\alpha_{I S}\) and the short-run equilibrium level of output?
e. Use Eq. (11.C.5) to compute the government purchases multiplier. Use your answer to compute the short-run change in \(Y\) resulting from an increase in government purchases from \(G=150\) to \(G=250\). How does your answer here compare to your answer in part \((d)\) ?
Eq. (11.C.5)
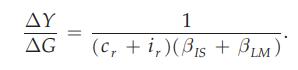
Step by Step Answer:






