(a) The Argonaut Company makes three products, Xylos, Yo-yos and Zicons. These are assembled from two components,...
Question:
(a) The Argonaut Company makes three products, Xylos, Yo-yos and Zicons. These are assembled from two components, Agrons and Bovons, which can be produced internally at a variable cost of £5 and £8 each respectively. A limited quantity of each of these components may be available for purchase from an external supplier at a quoted price which varies from week to week.
The production of Agrons and Bovons is subject to several limitations. Both components require the same three production processes (L, M and N), the first two of which have limited availabilities of 9600 minutes per week and 7000 minutes per week respectively. The final process (N) has effectively unlimited availability but for technical reasons must produce at least one Agron for each Bovon produced.
The processing times are as follows:
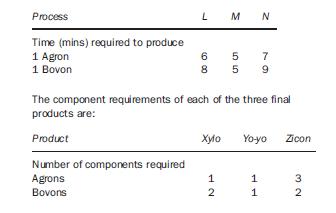
The ex-factory selling prices of the final products are given below, together with the standard direct labour hours involved in their assembly and details of other assembly costs incurred:

The standard direct labour rate is £10 per hour. Factory overhead costs amount to £4350 per week and are absorbed to products on the basis of the direct labour costs incurred in their assembly. The current production plan is to produce 100 units of each of the three products each week.
Requirements:
(i) Present a budgeted weekly profit and loss account, by product, for the factory.
(ii) Formulate the production problem facing the factory manager as a linear program:
1 assuming there is no external availability of Agrons and Bovons;
and 2 assuming that 200 Agrons and 300 Bovons are available at prices of £10 and £12 each respectively.
(b) In a week when no external availability of Agrons and Bovons was expected, the optimal solution to the linear program and the shadow prices associated with each constraint were as follows:
If sufficient Bovons were to become available on the external market at a price of £12 each, a revised linear programming solution indicated that only Xylos should be made.
Requirement:
Interpret this output from the linear program in a report to the factory manager. Include calculations of revised shadow prices in your report and indicate the actions the manager should take and the benefits that would accrue if the various constraints could be overcome.
Step by Step Answer:






