Every summer, the touring company America by Bicycle conducts the Cross Country Challenge, a 7-week bicycle journey

Question:

Every summer, the touring company America by Bicycle conducts the €œCross Country Challenge,€ a 7-week bicycle journey across the United States from San Francisco, California, to Portsmouth, New Hampshire. At some point during the trip, the exhausted cyclists usually start to complain that the organizers are purposely planning for days with lots of hill and mountain climbing to coincide with longer distances. The tour staff counter that no relation exists between climbs and mileage and that the route is organized based on practical issues, such as the location of towns in which riders can stay. The organizers who planned the route (these are the company owners who are not on the tour) say that they actually tried to reduce the mileage on the days with the worst climbs. Here are the approximate daily mileages and climbs (in vertical feet), as estimated from one rider€™s bicycle computer.

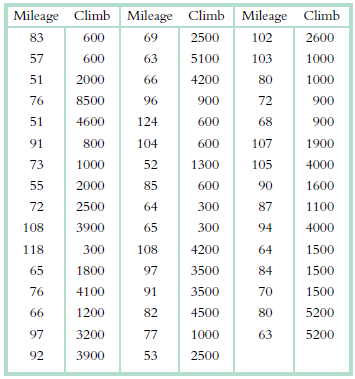
Mileage Climb Mileage Climb Mileage Climb 83 600 69 2500 102 2600 57 600 63 5100 103 1000 51 2000 66 4200 80 1000 76 850

a. Construct a scatterplot of the cycling data, putting mileage on the x-ax is. Be sure to label everything and include a title.

b. We haven€™t yet learned to calculate inferential statistics on these data, so we can€™t estimate what€™s really going on, but do you think that the amount of vertical climb is related to a day€™s mileage? If yes, explain the relation in your own words. If no, explain why you think there is no relation.

c. It turns out that inferential statistics do not support the existence of a relation between these variables and that the staff seems to be the most accurate in their appraisal. Why do you think the cyclists and organizers are wrong in opposite directions? What does this say about p eople€™s biases and the need for data?