Consider the equation for the par swap rate under OIS discounting in Section 12.1.3. If the OIS-Libor
Question:
Consider the equation 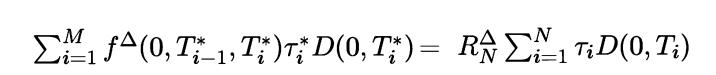
for the par swap rate under OIS discounting in Section 12.1.3. If the OIS-Libor spread is zero, show that this reduces to the classical equation D(0,T0) – D (0, TN) = ![]() Suppose that the OIS-Libor spread is a constant s, i.e.
Suppose that the OIS-Libor spread is a constant s, i.e. ![]() Express the swap rate RΔN in terms of the classical swap rate RN and the spread s.
Express the swap rate RΔN in terms of the classical swap rate RN and the spread s.
Section 12.1.3.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





