For large numbers of degrees of freedom, we can approximate critical values of x2 as follows:

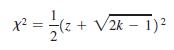
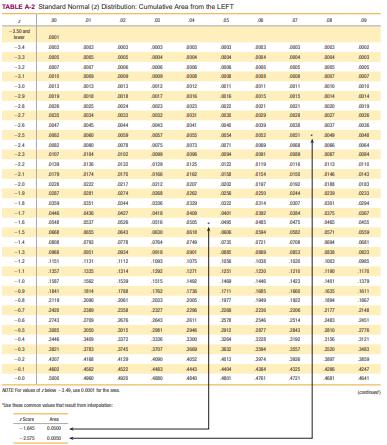
Here k is the number of degrees of freedom and z is the critical value(s) found from technology or Table A-2. In Exercise 12 “Spoken Words” we have df = 55, so Table A-4 does not list an exact critical value. If we want to approximate a critical value of x² in the right-tailed hypothesis test with α = 0.01 and a sample size of 56, we let k = 55 with z = 2.33 (or the more accurate value of z = 2.326348 found from technology). Use this approximation to estimate the critical value of x² for Exercise 12. How close is it to the critical value of x² = 82.292 obtained by using Statdisk and Minitab?

Table A-2:

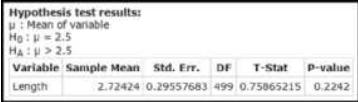
Data From Exercise 12:

Data Set 22 “Tornadoes” in Appendix B includes data from 500 random tornadoes. The accompanying StatCrunch display results from using the tornado lengths (miles) to test the claim that the mean tornado length is greater than 2.5 miles.

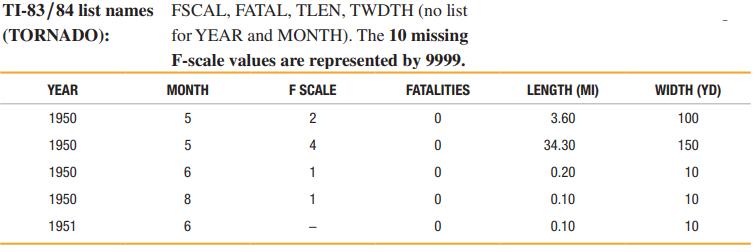
Data Set 22: Tornadoes 

Data are from 500 tornadoes (first five rows shown here) arranged chronologically. MONTH is the month of the tornado (1 = January), F SCALE is the Fujita scale rating of tornado intensity, FATALITIES is number of deaths caused by the tornado, LENGTH (MI) is the distance the tornado traveled in miles, and WIDTH (YD) is the tornado width in yards. Data are from the National Weather Service.