A mass \(m\) lies on a table and is connected to a string of length \(\ell\) as shown in Figure 10. 45. The string passes through a hole in the table and is connected to another mass \(M\) that is hanging in the air. We assume that the string remains taught and that mass \(M\) can only move vertically.

a. The Lagrangian for this setup is

\[\mathcal{L}=\frac{1}{2} M \dot{r}^{2}+\frac{1}{2} m\left(\dot{r}^{2}+r^{2} \dot{\theta}^{2}\right)+M g(\ell-r)\]

where \(r\) and \(\theta\) are polar coordinates describing where mass \(m\) is on the table with respect to the hole. Explain why the terms in the Lagrangian are appropriate.

b. Derive the equations of motion for \(r(t)\) and \(\theta(t)\).

c. What angular velocity is needed for mass \(m\) to maintain uniform circular motion?

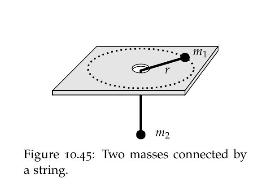
M2 m Figure 10.45: Two masses connected by a string.