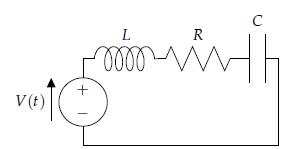
Question: Consider the series circuit in Problem 2. 20 and in Figure 2. 7 with (L=) (1.00 mathrm{H}, R=1.00 times 10^{2} Omega, C=1.00 times 10^{-4} mathrm{~F}),
Consider the series circuit in Problem 2. 20 and in Figure 2. 7 with \(L=\) \(1.00 \mathrm{H}, R=1.00 \times 10^{2} \Omega, C=1.00 \times 10^{-4} \mathrm{~F}\), and \(V_{0}=1.00 \times 10^{3} \mathrm{~V}\).
a. Write the second-order differential equation for this circuit.
b. Suppose that no charge is present and no current is flowing at time \(t=0\) when \(V_{0}\) is applied. Use Laplace transforms to find the current and the charge on the capacitor as functions of time.
c. Replace the battery with the alternating source \(V(t)=V_{0} \sin 2 \pi f t\) with \(V_{0}=1.00 \times 10^{3} \mathrm{~V}\) and \(f=150 \mathrm{~Hz}\). Again, suppose that no charge is present and no current is flowing at time \(t=0\) when the AC source is applied. Use Laplace transforms to find the current and the charge on the capacitor as functions of time.
d. Plot your solutions, and describe how the system behaves over time.
Data from Problem 2.20
Find the inverse Laplace transform in two different ways:
(i) Use tables.
(ii) Use the Bromwich Integral.
Data from Figure 2.7
V(t) C +
Step by Step Solution
3.34 Rating (148 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


