For spherical coordinates,

\[\begin{align*} x & =ho \sin \theta \cos \phi \\ y & =ho \sin \theta \sin \phi \\ z & =ho \cos \theta \tag{9.133} \end{align*}\]

find the scale factors and derive the following expressions:

\[\begin{gather*} abla f=\frac{\partial f}{\partial ho} \hat{\mathbf{e}}_{ho}+\frac{1}{ho} \frac{\partial f}{\partial \theta} \hat{\mathbf{e}}_{\theta}+\frac{1}{ho \sin \theta} \frac{\partial f}{\partial \phi} \hat{\mathbf{e}}_{\phi} \tag{9.134}\\ abla \cdot \mathbf{F}=\frac{1}{ho^{2}} \frac{\partial\left(ho^{2} F_{ho}\right)}{\partial ho}+\frac{1}{ho \sin \theta} \frac{\partial\left(\sin \theta F_{\theta}\right)}{\partial \theta}+\frac{1}{ho \sin \theta} \frac{\partial F_{\phi}}{\partial \phi} \tag{9.135} \end{gather*}\]

\[\begin{align*} abla \times \mathbf{F}= & \frac{1}{ho \sin \theta}\left(\frac{\partial\left(\sin \theta F_{\phi}\right)}{\partial \theta}-\frac{\partial F_{\theta}}{\partial \phi}\right) \hat{\mathbf{e}}_{ho}+\frac{1}{ho}\left(\frac{1}{\sin \theta} \frac{\partial F_{ho}}{\partial \phi}-\frac{\partial\left(ho F_{\phi}\right)}{\partial ho}\right) \hat{\mathbf{e}}_{\theta} \\ & +\frac{1}{ho}\left(\frac{\partial\left(ho F_{\theta}\right)}{\partial ho}-\frac{\partial F_{ho}}{\partial \theta}\right) \hat{\mathbf{e}}_{\phi} . \tag{9.136}\\ abla^{2} f= & \frac{1}{ho^{2}} \frac{\partial}{\partial ho}\left(ho^{2} \frac{\partial f}{\partial ho}\right)+\frac{1}{ho^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial f}{\partial \theta}\right)+\frac{1}{ho^{2} \sin ^{2} \theta} \frac{\partial^{2} f}{\partial \phi^{2}} . \tag{9.137} \end{align*}\]

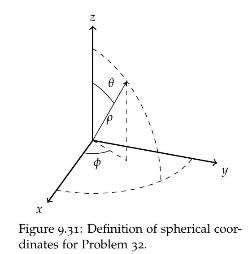
x Figure 9.31: Definition of spherical coor- dinates for Problem 32.