You will compute the (Fourier) convolution of two box functions of the same width. Recall that the box function is given by

\[f_{a}(x)= \begin{cases}1, & |x| \leq a \\ 0, & |x|>a\end{cases}\]

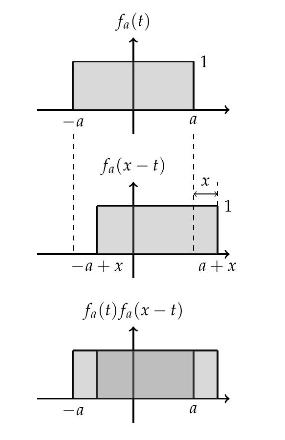
Consider \(\left(f_{a} * f_{a}\right)(x)\) for different intervals of \(x\). A few preliminary sketches will help. In Figure 8. 48, the factors in the convolution integrand are shown for one value of \(x\). The integrand is the product of the first two functions. The convolution at \(x\) is the area of the overlap in the third figure. Think about how these pictures change as you vary \(x\). Plot the resulting areas as a function of \(x\). This is the graph of the desired convolution.

a fa(t) fa(x-t) -a+x fa(t)fa(x-t) a -a a 1 a+x