Assume that the dynamics of the short rate process under the risk neutral measure is governed by

Question:

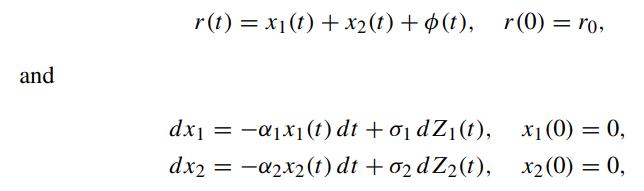
and r(t) = x(t) + x2(t)+p(t), r(0): dx = = -x (1) dt+odZ(t), dx2 = -a2x2 (1) dt +02dZ2(t), = ro, x(0) = 0,

with dZ₁(t)dZ₂(t) = ρdt. Show that the time-t price of a unit par discount bond is given by

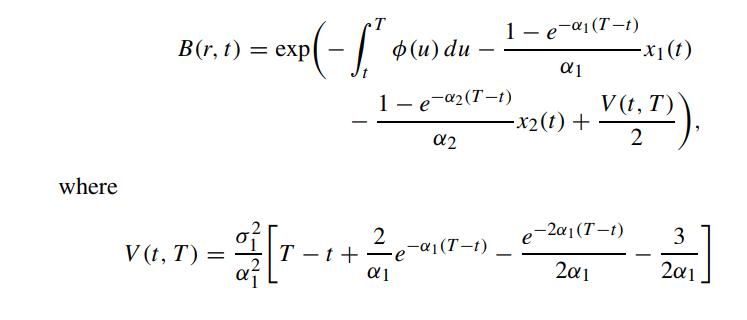
where B(r, t) = expl V(t, T) = T = exp(- [ [r 2 T-t+ (u) du 2 e 1 - 1 - e-a(T-1) 2 1- e- (T-1) - (T-1) -x2

+ + T-t+ 200102 [T 2-2 2 ,-2(T t) T-1 + - e-(T-1) e-(2)(T-t) + 2 e-a2(T-t) 22 - 3 202 1 e-a2(T-t) + - 1

Let f_m(0,T) denote the term structure of the forward rates at time 0 for maturity T as implied by the market bond prices. Show that the parameter function ∅(t) can be calibrated to f_m(0,T) via the relation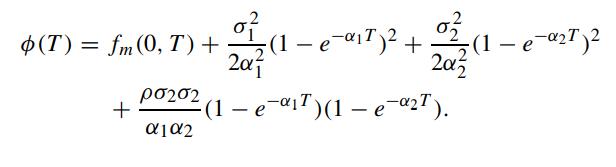 (T) = fm (0, T) + + 2 (1 e-T)2 + 20 20 (1 e-)(1 e-). (1 e-a2T)2