Consider an American call option with a continuously changing strike price X() where dX()/d Define the following

Consider an American call option with a continuously changing strike price X(τ) where dX(τ)/dτ

Define the following new set of variables:

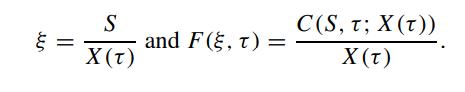
Show that the governing equation for the price of the above American call is given by 

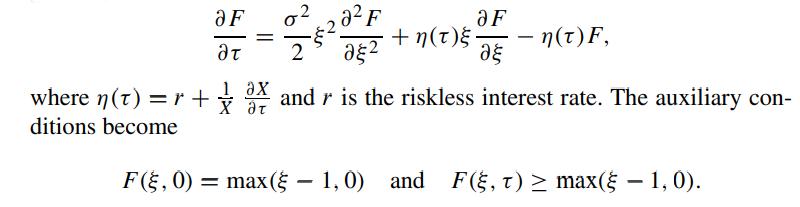
Show that if X(τ) ≥ X(0)e−rτ , then it is never optimal to exercise the American call prematurely. In such a case, show that the value of the above American call is the same as that of a European call with a fixed strike price X(0) (Merton, 1973, Chap. 1).

Show that when the time dependent function η(τ) satisfies the condition ∫^τ₀ η(s) ds ≥ 0, it is then never optimal to exercise the American call prematurely.

Transcribed Image Text:

and C(S, t; X(t)) ≥ max(S – X(t), 0) - C(S, T; X (0)) = max(SX (0), 0).