Consider the three-factor stochastic volatility model [see (7.3.17)], by assuming constant market prices of risk r
Question:
Consider the three-factor stochastic volatility model [see (7.3.17)], by assuming constant market prices of risk λr,λr and λv, show that the bond price function B(t, T) satisfies the partial differential equation
![a B = va2B 2v JB n 2 2 0 2 + - - + 2 272 2 8r2 aB +[a(r-r) - 2rvo] B + [r (U - v) - hus Vo]- - 22 B r v](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/6/2/8/147655d86b3894661700628144254.jpg) Suppose the discount bond price function admits the following exponential affine term structure
Suppose the discount bond price function admits the following exponential affine term structure
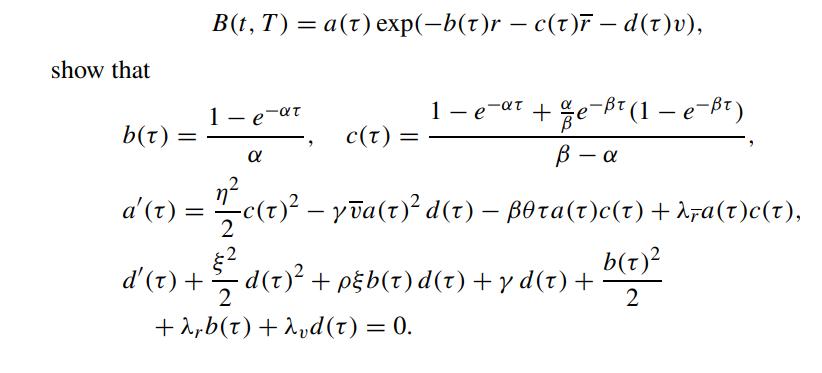
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





