From the BlackScholes price function c(S,) for a European vanilla call, show that the limiting values of

From the Black–Scholes price function c(S,τ) for a European vanilla call, show that the limiting values of the call price at vanishing volatility and infinite volatility are the lower and upper bounds of the European call price respectively, namely,

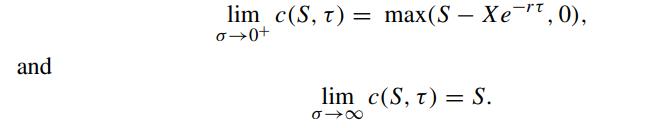
Give an appropriate financial interpretation of the above results. Apparently, X does not appear in c(S,τ) when σ →   ∞. Is it justifiable based on financial intuition?

Transcribed Image Text:

and lim c(S, T) = max(S - Xet, 0), +0+0 lim c(S, T) = S. 818