Let the stochastic process X(t),t 0, be defined by where Z(t) is the standard Brownian process.

Question:

Let the stochastic process X(t),t ≥ 0, be defined by

= [ eu(1-4), S 10 X (t) = ea(t-u) dz(u),

where Z(t) is the standard Brownian process. Show that

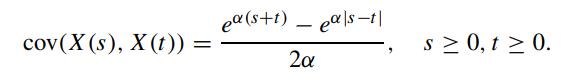
cov (X (s), X(t)) = ea (s+1) - eals-t| 2 S 0, t 0.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Mathematical Models Of Financial Derivative

ISBN: 9783642447938

2nd Edition

Authors: Yue-Kuen Kwok

See More Books

Question Posted: Dec 02, 2023 03:16 AM

See More Questions

A private startup company has just gone public. It is not expected to pay any dividends for the first 2 years. It is then expected to pay dividends of $13 per share with 10% growth for 4 years. After...
As a project manager, what project component should you focus on to minimize the likelihood of incurring changes to the project budget or extensions in the project timeline?
5. A corporation has 1,000 shares of stock outstanding. One person owns 60% of the stock and the minority stockholders together own the other 40% of the stock. If the company is voting for 10...
Your parents have made you an offer you can't refuse. They're planning to give you part of your inheritance early. They've given you a choice. Option (a) They'll pay you $11,000 per year for each of...
What are Nordstroms greatest risks, and who are its biggest competitors?
Critically evaluate the audit work of Ernst & Young from the perspective of generally accepted auditing standards and professional ethics. Was this a failed audit?
Evaluate all base classifier models and all voting ensemble models with respect to overall error rate, sensitivity, specificity, proportion of false positives, and proportion of false negatives....
Which of the many purposes of the project portfolio process are most important to a firm with a low project management maturity? Which to a firm with high maturity?
From the following data ,find the value of inventry as on 30.04.2009 using FIFO method : 1.04.2009 purchased 10 units @ 70 per unit 6.04.2009 sold 6 units @90 per unit 9.04.2009 purchased 20 units...
Let Z(t) denote the standard Brownian process. Show that (a) dZ(t) 2+n = 0, for any positive integer n, (b) for any positive integer n, (c) E[Z 4 (t)] = 3t 2 , (d) E[e Z (t) ] = e 2t / 2 . S to...
Consider the Brownian process with drift defined by where Z(t) is the standard Brownian process, find E[X(t)|X(t 0 )], var(X(t)| X(t 0 )) and cov(X(t 1 ), X(t 2 )). X(t)= ut +oZ(t), X(0) = 0,
A point isotropic sound source is located on the perpendicular to the plane of a ring drawn through the centre O of the ring. The distance between the point O and the source is l = |.00 m, the radius...
Albert is in third grade and has documented impulsivity issues in class. Develop a plan to teach Albert how to answer questions in class appropriately. He will currently shout out answers and if the...
What type of atmosphere is generated in the zara locations? How do the stores draw in their customers? Is there any atmospherics that would make you stay in the stores? Is it enjoyable inside, does...
You've been asked to create a machine learning service that helps people choose what concert to attend on a particular date based on the type of music they prefer, who is singing, and where the event...
What are the lessons (human resource, marketing, services, location, pricing, etc.) that Disney learned from its previous international ventures (Japan, EDL, HK)? What were some of the mistakes and...
17.C. a. A person asks you to convert a given point (x,y) into polar coordinates (r, 0). Explain how this might be an ambiguous question (i.e., is further information needed?). b. There is only 1 out...
Find the fourth order Macluarin polynomial for 1n[(1 + x) / (1 - x)] And bound the error R4(x) for -0.5 ( x ( 0.50?
Design and describe an application-level protocol to be used between an automatic teller machine and a bank's centralized computer. Your protocol should allow a user 's card and password to be...
Would you expect to find any wholesalers selling the various types of business products? Are retail stores required (or something like retail stores)?
What kinds of business products are the following: ( a ) lubricating oil, ( b ) electric motors, and ( c ) a firm that provides landscaping and grass mowing for an apartment complex? Explain your...
How do raw materials differ from other business products? Do the differences have any impact on their marketing mixes? If so, what specifically?
In 2019, Sunland Company had a break-even point of $388,000 based on a selling price of $5 per unit and fixed costs of $155,200. In 2020, the selling price and the variable costs per unit did not...
11. String Conversion Given a binary string consisting of characters '0's and '1', the following operation can be performed it: Choose two adjacent characters, and replace both the characters with...
Consider the table shown below to answer the question posed in part a. Parts b and c are independent of the given table. Callaway Golf (ELY) Alaska Air Group (ALK) Yum! Brands (YUM) Caterpillar...

Let the stochastic process X(t),t 0, be defined by where Z(t) is the standard Brownian process.

Question:

= [₁ eu(1-4), S 10 X(t) = ea(t-u) dz(u),

Step by Step Answer:

To find the covariance between X s and X t we need to compute covXs Xt ...View the full answer

Mathematical Models Of Financial Derivative

Students also viewed these Business questions